Examples of Variational Calculus

In the previous lesson, we discussed the Euler-Lagrange equation and the Beltrami identity in somewhat abstract terms. The goal of this lesson, on the other hand, is to answer the question “how do we use these concepts in practice?”.

Throughout this lesson, we will look at examples of applying calculus of variations to various situations. This will hopefully give you a concrete idea of how the tools of variational calculus, like the Euler-Lagrange equation, are actually used in practice.

The examples we look at are geared towards physical applications, but of course, all of them are really just examples of applying the math we’ve learned so far. I’ve tried to include examples that are as interesting and as easily applicable to other areas of physics and math as possible.

The basic framework or “recipe” for solving a calculus of variations problem that we’ll use in these example applications is more or less as prescribed below.

F=\int_{x_1}^{x_2}f\left(x{,}\ y{,}\ y'\right)dx

\frac{d}{dx}\frac{\partial f}{\partial y'}-\frac{\partial f}{\partial y}=0

Lesson Contents

Geodesics

Our first application of variational calculus will be more of a math-focused one, but it has some incredibly important applications to, for example, general relativity.

In particular, the application we will look at next is one of the most important ways in which calculus of variations shows up in other areas of math and physics and that is to find paths that minimize the distance between two points on some surface. These paths of minimum distance between two points are called geodesics.

When we typically think of two points and some path joining them, a straight line naturally comes to mind – the shortest distance between two points is a straight line.

However, this is only true when we talk about a flat geometry, such as a plane. If we’re on the surface of some complicated geometry, geodesics – the paths of minimum distance between any two points, work somewhat differently.

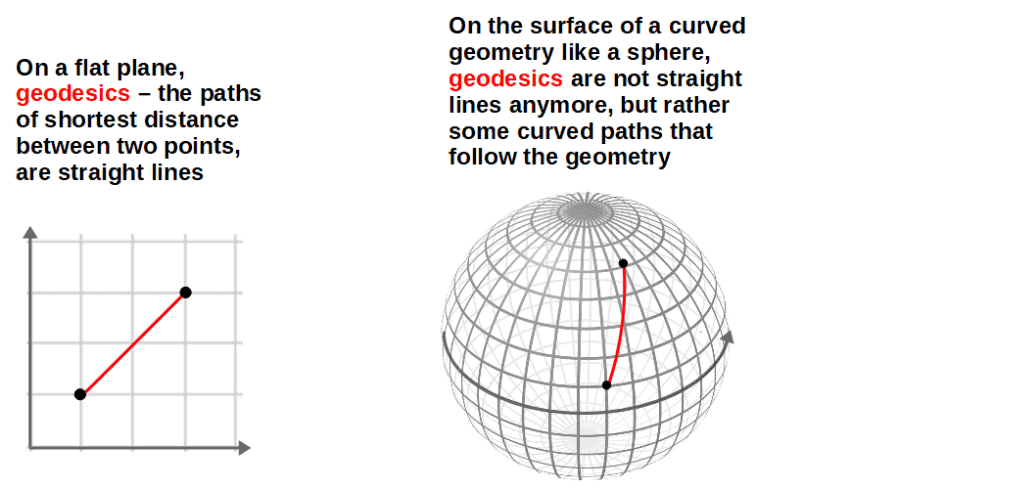
It’s worth noting that if you were to be living on this curved surface (sphere, for example), and began walking along a geodesic, it would appear to you as if you were moving in a straight line. So, the concept of a straight line being the shortest distance between two points is still kind of true if you are constrained to be on the surface itself.

It is only when we zoom out and look at the geometry from an “outside” perspective, we see that the geodesics are actually not straight lines, at least not “as straight” as they would be on a plane.

In fact, this idea is sometimes taken to explain what a geodesic is – a geodesic is the “straightest possible line” between two points on a surface. This statement can also be made rigorous through a concept called parallel transport, which will likely come up if you study differential geometry.

Now, how does all of this relate to calculus of variations? Well, we describe distances along surfaces by integrating along some curve on the surface. These integrals describing distances generally have the form of a functional.

Then, if we want to minimize these distance functionals (find the shortest possible distances – geodesics), we use the tools of variational calculus like the Euler-Lagrange equation. This naturally lends the problem of finding geodesics to calculus of variations.

Let’s now look at how finding these geodesics works in practice and in a later lesson, we will look at how this can also be applied to general relativity. In particular, we’ll look at two examples here:

Geodesics on a plane – these turn out to be straight lines as we would expect, but we’ll see how exactly this comes about using calculus of variations.
Geodesics on a sphere – these turn out to be arcs along a great circle, which we can also derive using calculus of variations.

Essentially, the plan is to first look at the mathematical description of why exactly the shortest distance between two points is a straight line – yes, this may seem obvious, but it’s worth looking at this from a rigorous mathematical perspective first. This will allow us to understand how the concept of geodesics is generalized to more complicated geometries than just a flat plane.

After the simple flat plane example, we will ask the question “what if the path between two points is constrained to be on some surface other than a plane, such as a sphere? What do the geodesics look like then?”.

Geodesics On a Plane

So, we want to begin by finding the path of shortest distance between two points – a geodesic – on a plane. We can describe the situation using the standard Cartesian x,y -coordinate grid.

First, we need to find a functional that describes the length of this path, the distance from a to b. We can then use the Euler-Lagrange equation (or Beltrami identity) to find the curve y(x) in the x,y -plane that minimizes this distance between the two points.

The key to this is that no matter which curve we have between the two points a and b, we can always break it down into small small “pieces of distance” along the curve:

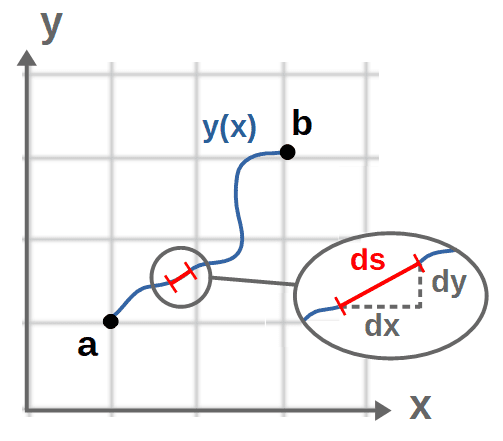
If these ds-pieces are small enough (infinitesimal, to be precise), they look exactly like straight lines and we can apply the Pythagorean theorem:

ds^2=dx^2+dy^2\ \ \Rightarrow\ \ ds=\sqrt{dx^2+dy^2}

This describes a small distance along any curve y(x) on the x,y -plane. We can then get the total distance s between the points a and b by integrating all these ds-pieces:

This might look like a weird thing to write down since we don’t have anything we’d be integrating with respect to here. We can “fix” this by factoring out dx² from inside the square root:

s=\int_a^b\sqrt{dx^2\left(1+\frac{dy^2}{dx^2}\right)}=\int_a^b\sqrt{1+\left(\frac{dy}{dx}\right)^2}dx

Here, dy/dx is just the derivative of y(x), which we’ll denote as y’.

We now have a functional that gives us the distance s along any curve y(x) between the two points a and b:

This expression is typically called the arc length formula as it can be used to calculate arc length of a curve between two points.

Now, to find the curve y(x) that minimizes the distance s, we use either the Euler-Lagrange equation or the Beltrami identity on the integrand (the Beltrami identity is valid here since our integrand does not explicitly depend on x):

I’ll choose to use the Beltrami identity here since it’s a lot simpler (however, the Euler-Lagrange equation would get you to the exact same result). From it, we get using the chain rule:

\Rightarrow\ \ \frac{\partial}{\partial y'}\left(\sqrt{1+y'^2}\right)y'-\sqrt{1+y'^2}=C

\Rightarrow\ \ \frac{1}{2\sqrt{1+y'^2}}\cdot\frac{\partial}{\partial y'}\left(1+y'^2\right)y'-\sqrt{1+y'^2}=C

\Rightarrow\ \ \frac{1}{2\sqrt{1+y'^2}}\cdot2y'\cdot y'-\sqrt{1+y'^2}=C

\Rightarrow\ \ \frac{y'^2}{\sqrt{1+y'^2}}-\sqrt{1+y'^2}=C

We can then multiply everything by √(1+y’²) to get:

y'^2-\left(\sqrt{1+y'^2}\right)^2=C\sqrt{1+y'^2}

\Rightarrow\ \ y'^2-\left(1+y'^2\right)=C\sqrt{1+y'^2}

Solving this for y’=dy/dx, we get:

This whole square root thing on the right-hand side is just another arbitrary constant (because C is arbitrary) that we can call A, so we just have:

Then, all we do is integrate both side and add an integration constant B to get:

This, of course, is the equation for a straight line, which is exactly what we were expecting – the shortest distance between two points on a plane is a straight line. This was the variational method to derive this result.

Geodesics On a Sphere

Now, let’s do the same we did above but now for a sphere. In other words, we want to find the geodesics, paths of shortest distance between two points a and b, along the surface of a sphere of some radius R.

We can describe points on the surface of the sphere by labeling two angles, θ and φ. These are enough to determine any point on the surface since the distance to the center is always the same (R):

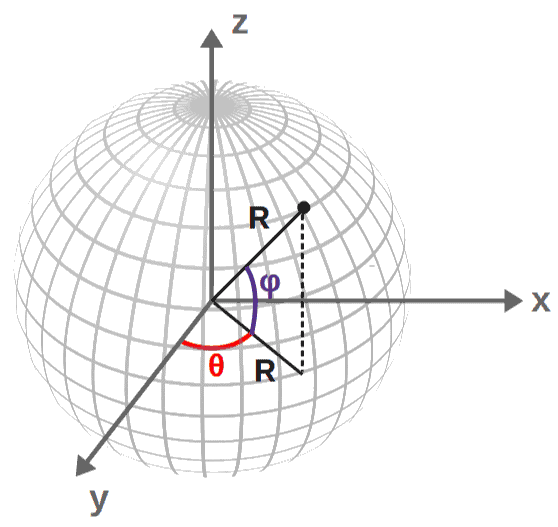
Now, how do we describe distances between points on the sphere’s surface? Well, we can do this by using spherical coordinates – if you’ve noticed, these angles θ and φ are exactly the two angular coordinates in spherical coordinates.

First, we need to “convert” distances in Cartesian coordinates to distances in spherical coordinates. This is because Cartesian coordinates don’t work very well for a spherical geometry like this and we wouldn’t be able to get anything useful out of using them.

Luckily, we already know the formula for distance in Cartesian coordinates – any path between two points can be “broken down” into small pieces with length ds given by the Pythagorean theorem (this is exactly what we did in the “geodesics on a plane” -example):

Now we just need to convert from these dx, dy and dz -coordinate displacements to the spherical coordinate displacements dθ and dφ. The first thing we do is use the relation between Cartesian and spherical coordinates:

Here, we have x, y and z as functions of the coordinates θ and φ. If we want to find the change in, say x(θ,φ), we use the formula for the differential of a multivariable function:

dx=\frac{\partial x}{\partial\theta}d\theta+\frac{\partial x}{\partial\varphi}d\varphi

We essentially have the “rates of change in x times the change in the coordinates”. These partial derivatives we can find by simply taking partial derivatives of the relation above, x=Rcosθsinφ. Doing this, we get:

dx=\frac{\partial x}{\partial\theta}d\theta+\frac{\partial x}{\partial\varphi}d\varphi=-R\sin\theta\sin\varphi d\theta+R\cos\theta\cos\varphi d\varphi

We can repeat the same steps to get dy and dz:

dy=\frac{\partial y}{\partial\theta}d\theta+\frac{\partial y}{\partial\varphi}d\varphi=R\cos\theta\sin\varphi d\theta+R\sin\theta\cos\varphi d\varphi

dz=\frac{\partial z}{\partial\theta}d\theta+\frac{\partial z}{\partial\varphi}d\varphi=-R\sin\varphi d\varphi

With these, we can now write ds (or ds² here) in terms of these spherical coordinate displacements as:

=\left(-R\sin\theta\sin\varphi d\theta+R\cos\theta\cos\varphi d\varphi\right)^2+\left(R\cos\theta\sin\varphi d\theta+R\sin\theta\cos\varphi d\varphi\right)^2+\left(-R\sin\varphi d\varphi\right)^2

This is a somewhat complicated looking thing but luckily, we can simplify it a lot. First, let’s write out all these squares to get:

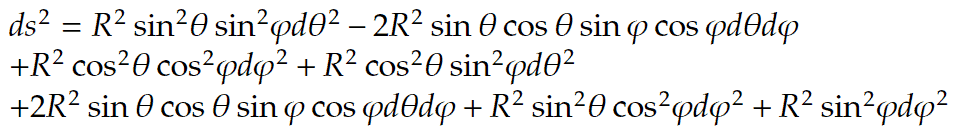
Here, the cross-terms with both dθ and dφ cancel out. We can also combine and factor some of the terms to end up with:

ds^2=\left(\sin^2\theta+\cos^2\theta\right)R^2\sin^2\varphi d\theta^2+\left(\left(\sin^2\theta+\cos^2\theta\right)\cos^2\varphi+\sin^2\varphi\right)R^2d\varphi^2

Now we just use the fact that cos²θ+sin²θ=1 (and similarly for φ as well) to get:

ds^2=R^2\sin^2\varphi d\theta^2+\left(\cos^2\varphi+\sin^2\varphi\right)R^2d\varphi^2=R^2\sin^2\varphi d\theta^2+R^2d\varphi^2

We can then get ds as:

ds=\sqrt{R^2\sin^2\varphi d\theta^2+R^2d\varphi^2}=R\sqrt{1+\sin^2\varphi\left(\frac{d\theta}{d\varphi}\right)^2}d\varphi

Here I’ve factored out R²dφ² from inside the square root, similarly to what we did with dx in the previous straight line example. The total distance between any two points a and b is then given by integrating ds. This gives us a functional s(θ):

s\left(\theta\right)=\int_a^bds=R\int_a^b\sqrt{1+\sin^2\varphi\left(\frac{d\theta}{d\varphi}\right)^2}d\varphi

Now, what have we done here? We’ve found a formula that describes the distance between any two points on the surface of a sphere. In particular, s(θ) here describes the distance along a curve θ(φ) on the sphere’s surface.

This curve, θ(φ), describes one of the angles (θ) as a function of the other angle (φ). In other words, the curve θ(φ) describes a set of points – a curve – between the points a and b, just like y(x) did in Cartesian coordinates. We just have different variables here.

Now, if we want to find the minimum distance between a and b, we have to find the curve θ(φ) that minimizes the distance s(θ). Well, we use calculus of variations to do that!

In particular, we have to use the Euler-Lagrange equation (the Beltrami identity doesn’t apply here since our functional depends explicitly on φ – which plays the role of the variable x we had previously):

\frac{d}{d\varphi}\frac{\partial f}{\partial\theta'}-\frac{\partial f}{\partial\theta}=0

This f here is the integrand of our distance functional (with θ’=dθ/dφ):

Now, before we start plugging stuff into the Euler-Lagrange equation, we can notice that f does not depend on θ explicitly. This means that the partial derivative ∂f/∂θ=0 and we have from the Euler-Lagrange equation:

\frac{d}{d\varphi}\frac{\partial f}{\partial\theta'}-\frac{\partial f}{\partial\theta}=0\ \ \Rightarrow\ \ \frac{d}{d\varphi}\frac{\partial f}{\partial\theta'}=0

What does such an equation mean? Since the derivative of ∂f/∂θ’ is zero, it means that ∂f/∂θ’ itself is a constant. We can call this constant C:

This is what we have from the Euler-Lagrange equation! Let’s now calculate this partial derivative:

\frac{\partial f}{\partial\theta'}=\frac{\partial}{\partial\theta'}\left(R\sqrt{1+\theta'^2\sin^2\varphi}\right)

=\frac{R}{2\sqrt{1+\theta'^2\sin^2\varphi}}\cdot\frac{\partial}{\partial\theta'}\left(1+\theta'^2\sin^2\varphi\right)

=\frac{R}{2\sqrt{1+\theta'^2\sin^2\varphi}}\cdot2\theta'\sin^2\varphi

=\frac{R\theta'\sin^2\varphi}{\sqrt{1+\theta'^2\sin^2\varphi}}

We then have from the Euler-Lagrange equation:

\frac{R\theta'\sin^2\varphi}{\sqrt{1+\theta'^2\sin^2\varphi}}=C

Let’s manipulate this to a slightly different form. First, let’s multiply by this square root thing in the denominator and square both sides:

\frac{R\theta'\sin^2\varphi}{\sqrt{1+\theta'^2\sin^2\varphi}}=C\ \ \Rightarrow\ \ R^2\theta'^2\sin^4\varphi=C^2\left(1+\theta'^2\sin^2\varphi\right)

We can then solve this for θ’=dθ/dφ:

R^2\theta'^2\sin^4\varphi=C^2\left(1+\theta'^2\sin^2\varphi\right)

\Rightarrow\ \ \left(\frac{R^2}{C^2}\sin^2\varphi-1\right)\theta'^2\sin^2\varphi=1

\Rightarrow\ \ \frac{d\theta}{d\varphi}=\frac{1}{\sin\varphi\sqrt{\frac{R^2}{C^2}\sin^2\varphi-1}}

Here we have a differential equation that we could solve to get the curves θ(φ) of minimum distance between the two points a and b.

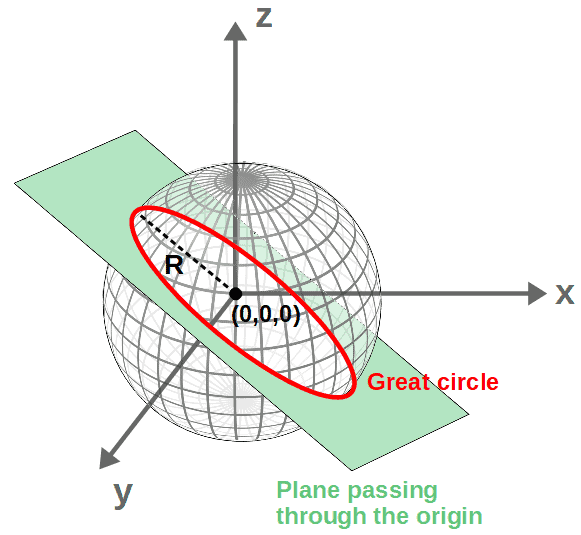
Now, these solutions you get for θ(φ) from this differential equation happen to describe curves called great circles. These are essentially circles around the sphere that are formed by “slicing” the sphere with a plane that passes through the origin (or more generally, a plane that passes through the center of the sphere if the sphere is centered somewhere other than the origin – here, however, we have a sphere with its center at the origin).

The intersection of these planes with the sphere’s surface then form great circles:

The full solution of the above differential equation as well as a proof that these curves are really great circles can be found below.

Solving The Great Circle Differential Equation

We essentially need to prove that the following differential equation, representing the geodesics on a sphere, describes great circles:

\frac{d\theta}{d\varphi}=\frac{1}{\sin\varphi\sqrt{\frac{R^2}{C^2}\sin^2\varphi-1}}

First, let’s integrate both sides with respect to φ:

\int_{ }^{ }\frac{d\theta}{d\varphi}d\varphi=\int_{ }^{ }\frac{1}{\sin\varphi\sqrt{\frac{R^2}{C^2}\sin^2\varphi-1}}d\varphi\ \ \Rightarrow\ \ \theta+A=\int_{ }^{ }\frac{1}{\sin\varphi\sqrt{\frac{R^2}{C^2}\sin^2\varphi-1}}d\varphi — This A here is an arbitrary integration constant.

To solve the right-hand side integral, we can use the definition of a trigonometric function called cosecant, which is defined as cosecφ=1/sinφ. Therefore, we can insert sinφ=1/cosecφ into this to get:

\int_{ }^{ }\frac{1}{\sin\varphi\sqrt{\frac{R^2}{C^2}\sin^2\varphi-1}}d\varphi=\int_{ }^{ }\frac{\operatorname{cosec}\varphi}{\sqrt{\frac{R^2}{C^2}\frac{1}{\operatorname{cosec}^2\varphi}-1}}d\varphi

Factoring out 1/cosec²φ from under the square root, we get:

\int_{ }^{ }\frac{\operatorname{cosec}\varphi}{\sqrt{\frac{1}{\operatorname{cosec}^2\varphi}\left(\frac{R^2}{C^2}-\operatorname{cosec}^2\varphi\right)}}d\varphi=\int_{ }^{ }\frac{\operatorname{cosec}^2\varphi}{\sqrt{\frac{R^2}{C^2}-\operatorname{cosec}^2\varphi}}d\varphi

There is also a nice trigonometric identity for the cosecant that we can take advantage of here – namely that cosec²φ=1+cot²φ, where cotφ is the cotangent function defined as 1/tanφ. Using this, we have:

\int_{ }^{ }\frac{\operatorname{cosec}^2\varphi}{\sqrt{\frac{R^2}{C^2}-\left(1+\cot^2\varphi\right)}}d\varphi

Now, we can use a clever trigonometric substitution here by defining a new variable u=cotφ. Then, by using the fact that the derivative of cotangent is -cosecant², we have:

du=\frac{du}{d\varphi}d\varphi=\frac{d}{d\varphi}\left(\cot\varphi\right)d\varphi=-\operatorname{cosec}^2\varphi d\varphi\ \ \Rightarrow\ \ d\varphi=-\frac{du}{\operatorname{cosec}^2\varphi}

Substituting this for dφ and u=cotφ into the integral above, we get:

\Rightarrow\ \ \int_{ }^{ }\frac{\operatorname{cosec}^2\varphi}{\sqrt{\frac{R^2}{C^2}-\left(1+u^2\right)}}\left(-\frac{du}{\operatorname{cosec}^2\varphi}\right)

\Rightarrow\ \ -\int_{ }^{ }\frac{1}{\sqrt{\frac{R^2}{C^2}-1-u^2}}du

We can define a new constant B here as B=R²/C²-1, so that we now have:

This is now a fairly basic integral you’ll find the solution to in any integration table. The solution is:

-\int_{ }^{ }\frac{1}{\sqrt{B-u^2}}du=-\arcsin\left(\frac{u}{\sqrt{B}}\right)

Substituting back in u=cotφ, we have the solution in terms of φ as:

-\int_{ }^{ }\frac{1}{\sqrt{B-u^2}}du=-\arcsin\left(\frac{\cot\varphi}{\sqrt{B}}\right)

So, finally, the solution to our original equation is:

\theta+A=\int_{ }^{ }\frac{1}{\sin\varphi\sqrt{\frac{R^2}{C^2}\sin^2\varphi-1}}d\varphi\ \ \Rightarrow\ \ \theta+A=-\arcsin\left(\frac{\cot\varphi}{\sqrt{B}}\right)

We can solve this to get the curve θ(φ) to be:

\theta\left(\varphi\right)=-\arcsin\left(\frac{\cot\varphi}{\sqrt{B}}\right)-A

Now, while this IS the solution to our geodesic problem on the sphere – meaning that these particular curves, θ(φ), describe the geodesics on the surface of the sphere – the form of this solution might not tell you anything. What do these curves even look like?

Well, it turns out that these curves θ(φ) describe great circles and the way to see this is by manipulating this expression into a “nicer” form as follows:

\theta\left(\varphi\right)=-\arcsin\left(\frac{\cot\varphi}{\sqrt{B}}\right)-A\ \ \Rightarrow\ \ -\sin\left(\theta+A\right)=\frac{\cot\varphi}{\sqrt{B}}

We can use a trigonometric identity here, which tells us that for any two variables, x₁ and x₂, the following is true:

\sin\left(x_1+x_2\right)=\sin x_1\cos x_2+\cos x_1\sin x_2

Applying this on the left-hand side, we get:

-\sin\theta\cos A-\cos\theta\sin A=\frac{\cot\varphi}{\sqrt{B}}

Let’s now multiply everything by sinφ:

-\cos A\sin\theta\sin\varphi-\sin A\cos\theta\sin\varphi=\frac{\cot\varphi\sin\varphi}{\sqrt{B}}

Since cotφ=1/tanφ=cosφ/sinφ, we have cotφsinφ = cosφ on the right-hand side. Now, as a reminder, we’re working in spherical coordinates here – θ and φ are the two spherical angles.

However, we can switch back to Cartesian coordinates by using the following relations between Cartesian and spherical coordinates (with the r-coordinate being a constant R, the radius of our sphere):

From these, we can get the following expressions:

Well, these are exactly what we have in our equation above that describes the geodesics on the sphere! Inserting these expressions, our equation then becomes:

-\cos A\sin\theta\sin\varphi-\sin A\cos\theta\sin\varphi=\frac{\cos\varphi}{\sqrt{B}}\ \ \Rightarrow\ \ -\cos A\frac{y}{R}-\sin A\frac{x}{R}=\frac{1}{\sqrt{B}}\frac{z}{R}

Cancelling out the R’s and moving all terms to one side, we finally get:

This has the form ax + by + cz = 0, since A and B here are just some arbitrary constants. What does such an equation describe? It describes a plane in three dimensions! And, not just any plane, but a plane that passes through the origin, since the point (0,0,0) satisfies the above relation.

What does this mean for our context of geodesics on the sphere? Well, the geodesics on the sphere must satisfy the equation of this plane passing through the origin – in other words, the geodesics must lie on a plane that passes through the origin.

On the other hand, the geodesics have to also lie on the sphere’s surface, so the actual geodesic curves along the surface of the sphere are therefore given by the intersections of this plane with the sphere’s surface – these are exactly great circles!

In terms of our solution, however, this means that the paths of shortest distance between the two points a and b – the geodesics we wanted to find – are great circles. Thus, all geodesics on a sphere are great circles or arcs of great circles – the curve doesn’t have to go around the sphere fully if the two points are close by.

So, if you have two points on a sphere and you want to find the shortest distance between them, just draw a plane that passes through the origin with both points lying on on this plane. The path of shortest distance is then given by the curve you get by looking at where the plane intersects the surface of the sphere between these points (which is an arc of a great circle):

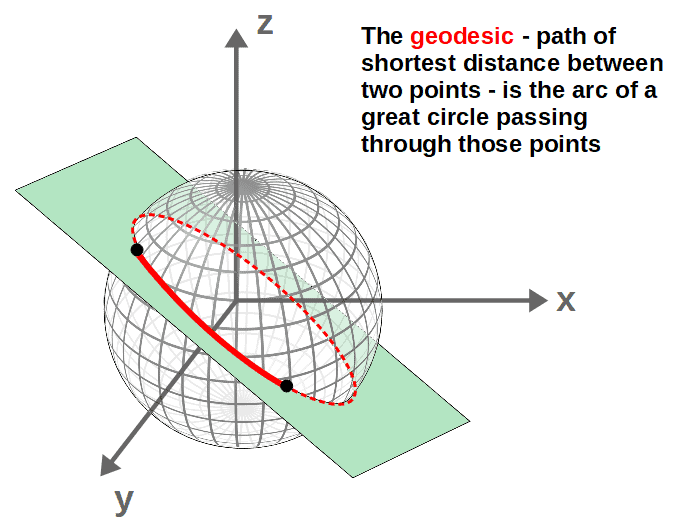
This also has some interesting real-world applications when looking at flight times and distances between different parts of Earth. For example, say we wanted to fly a plane from London to New York in the shortest possible flight time (assuming that the shortest flight time also corresponds to the shortest flight distance).

Since the Earth is pretty much a perfect sphere over large distances, the geodesics on Earth – shortest paths between points – are arcs along great circles. So, the shortest flight path between London and New York would NOT be to fly directly in a straight “line” but rather, along the arc of a great circle.

This is also why when we project the full spherical Earth onto a 2-dimensional flat map, it looks as if the shortest flight path would be a curved path:

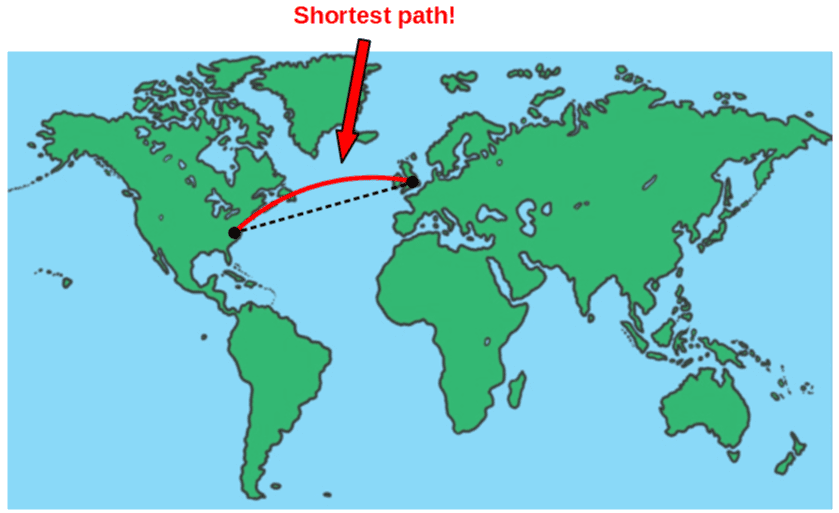
According to the picture, it would even seem that the geodesic (this curved path) is longer than the direct, straight line path. However, this is not the case in reality and now you know the reason why – it’s because geodesics are great circles and when projecting the surface of the spherical Earth onto a flat map, shapes get distorted and do not correspond to what is actually the case anymore.

Geodesics In Physics & Differential Geometry

Finding geodesics is incredibly important in areas of mathematics like differential geometry. In differential geometry, we’re often looking at spaces or geometries that can be described by a so-called metric tensor g_ij.

The metric tensor essentially allows us to describe all distances in a given space (such as on the surface of a sphere). The distance is given by a functional that has the following form:

s=\int_a^b\sqrt{g_{ij}\frac{dx^i}{d\lambda}\frac{dx^j}{d\lambda}}d\lambda — Note; in this expression, we’re using the Einstein summation convention, meaning that we’re actually summing over both the i and j indices here. This sum convention is discussed in the lesson on index notation.

Without getting into the details for now, this is essentially a generalization of the distance functionals we looked at earlier.

Now, using the Euler-Lagrange equation, it’s possible to derive a general equation that describes the curves of minimum distance between any two points. This is called the geodesic equation:

\frac{d^2x^i}{d\lambda^2}+\frac{1}{2}g^{ij}\left(\frac{\partial g_{jn}}{\partial x^m}+\frac{\partial g_{jm}}{\partial x^n}-\frac{\partial g_{mn}}{\partial x^j}\right)\frac{dx^m}{d\lambda}\frac{dx^n}{d\lambda}=0

While this equation might look complicated, it’s incredibly powerful – the geodesic equation is a general “formula” for calculating geodesics in any space with a metric. From this, we could directly find the geodesics on a sphere (for example), simply by inserting the metric tensor on a sphere.

The geodesic equation has applications in general relativity, among other thing. In general relativity, the paths that objects take through spacetime under the influence of gravity are always geodesics.

In other words, anything under the influence of gravity moves along a geodesic and the geodesic equation is used to calculate these paths by specifying a given spacetime metric. This can be used to predict the deflection of light around a star, orbits around a black hole as well as many other interesting things.

We will talk more about the applications of geodesics and variational calculus to general relativity in a later lesson, so we’re not going to go into any more detail here.

However, the key point here is that all of this is possible because we have the tools of variational calculus at our disposal. If it wasn’t for calculus of variations, we wouldn’t be able to find geodesics in such a nice and practical way.

So, at least if you’re planning to learn general relativity or differential geometry, I would highly recommend getting good at calculus of variations!

The Brachistochrone Problem

Our next example is most commonly known as the brachistochrone problem. This is one of my personal favourite problems in physics and it’s a great example of using the tools of variational calculus.

Essentially, the brachistochrone consists of a rollercoaster built between two points, a and b, with a constant gravitational acceleration g acting downwards. The shape of the rollercoaster is described by some curve y(x) in the x,y-plane:

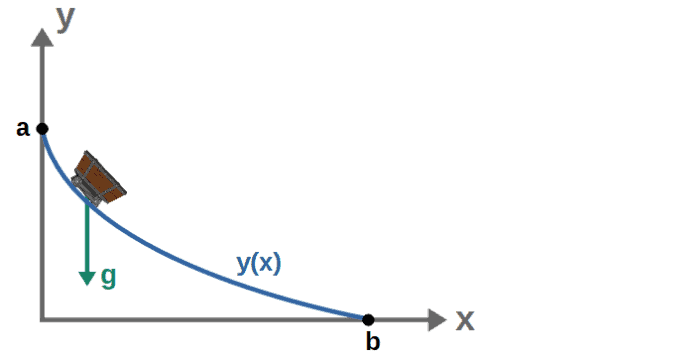
The goal of the brachistochrone problem is to find the minimum possible time in which the cart rolls down from point a and b and the shape of the curve y(x) that achieves this.

We’ll assume here that the track is frictionless and air resistance negligible.

The catch here is that as the cart is let to roll down along the rollercoaster track from the starting point a, its velocity will, of course, increase due to the influence of gravity. So, ideally we’d want to maximize this velocity – since gravity only acts downward, the track or curve y(x) should be as vertical as possible to maximize the velocity of the cart.

However, there is also the distance itself between the points a and b – this should be as short as possible for the “rolling time” to be minimized. Essentially, we have a trade-off between maximizing the velocity of the cart and minimizing the distance traveled – the goal is to find the “balance” between these two to achieve the shortest possible time.

This is then an optimization problem of finding the shape of the curve y(x) in which the cart achieves the largest velocity, while the distance between the two end points being as small as possible.

Naturally, this lends itself to be a calculus of variations problem, because the distance between any two points along a curve is generally described by a functional.

The first thing we’ll do is find the distance functional and then from that, a functional describing the rolling time of the cart which we want to minimize using the Euler-Lagrange equation. We’ll then get a differential equation we can solve for the curve y(x) to get the minimal rolling time.

Let’s get started! First, we need to find something that would describe the distance from a to b along the track, which is also the distance the cart rolls between these points since the cart moves along the curve y(x) at all times.

We can find a formula for the distance by breaking down the curve y(x) into small distance “pieces” ds. The distance ds is then just a “small piece” of the arc length of this curve. If we assume ds to be small enough (technically, we would take it to be “infinitesimally small”), it can be approximated by the Pythagorean theorem as:

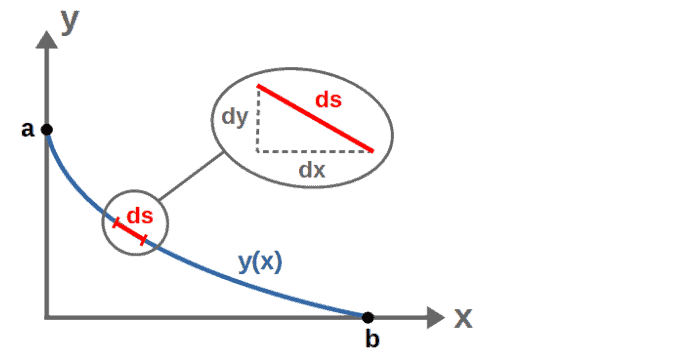
Let’s manipulate this expression a bit – first, take the square root of both sides (picking only the positive root, since we’re talking about distances here) and factor out a dx² from inside the square root:

ds=\sqrt{dx^2+dy^2}=\sqrt{dx^2\left(1+\left(\frac{dy}{dx}\right)^2\right)}=\sqrt{1+y'^2}dx — Here, I’m denoting dy/dx as y’.

This is our formula for the distance along a small piece of the arc length of the curve y(x). You might notice that this is exactly the same formula as the one we had in the “geodesics on a plane” -problem.

The total distance from a to b is then obtained by integrating (adding up) all of these pieces.

But first, let’s find an expression for the velocity of the cart at all points along the curve – we need this to find a functional describing the roll time.

We can use the conservation of energy here – the total energy E of the cart is conserved (since there are no non-conservative forces in this problem), so it is just some constant.

The total energy itself consists of a kinetic energy term T=1/2mv² and a potential energy term, given by the gravitational potential energy formula V=mgh.

Now, what is the height h of the cart here? It’s just the y-coordinate of the cart, which is also the y-coordinate of the curve, y(x). So, we have V=mgy and the total energy:

We can use this to find an expression for the velocity:

E=\frac{1}{2}mv^2+mgy\ \ \Rightarrow\ \ v=\sqrt{\frac{2E}{m}-2gy}

This now describes the velocity of the cart as a function of the curve y=y(x), in other words, the velocity of the cart at any point y(x) along the curve.

Now, we know that the velocity of the cart should also be the time derivative of the distance moved along the track, v=ds/dt.

We can “flip” this relation around to get an expression for a small time interval dt as the cart rolls along the track:

v=\frac{ds}{dt}\ \ \Rightarrow\ \ dt=\frac{ds}{v}

But, we know both the distance ds and the velocity v expressed in terms of y and y’. Inserting these, we have:

dt=\frac{ds}{v}=\frac{\sqrt{1+y'^2}dx}{\sqrt{\frac{2E}{m}-2gy}}=\sqrt{\frac{m}{2E}}\sqrt{\frac{1+y'^2}{1-\frac{mg}{E}y}}dx

The total roll time of the cart is then given by integrating this dt from a to b:

T=\int_a^bdt=\sqrt{\frac{m}{2E}}\int_a^b\sqrt{\frac{1+y'^2}{1-\frac{mg}{E}y}}dx

This has exactly the form of a functional written as a definite integral over some function f(y,y’)dx, which we want to minimize! Following the steps given earlier, we can identify the integrand here as:

f=\sqrt{\frac{m}{2E}}\sqrt{\frac{1+y'^2}{1-\frac{mg}{E}y}}

There are two ways to now obtain the differential equation minimizing this roll time – one is by directly plugging f into the Euler-Lagrange equation. However, the other one is by using the Beltrami identity, since f does not explicitly depend on x here.

My recommendation would be to use the Beltrami identity here, since it turns out to be much more simple.

However, to illustrate that this is indeed the easier way, you’ll find the same calculation done using both the Euler-Lagrange equation and the Beltrami identity down below (I recommend having a look at both of them to see how the Beltrami identity can really simplify calculations in some cases like this one).

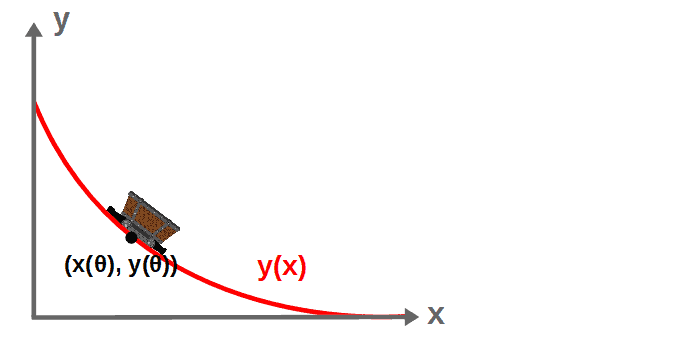
What we find is that the curve y(x) can be solved parametrically in terms of a curve parameter θ, in which case, the coordinates along the curve are given by:

x\left(\theta\right)=\frac{\alpha}{2}\left(\sin\theta-\theta\right)

y\left(\theta\right)=\beta-\alpha\sin^2\left(\frac{\theta}{2}\right) — Here, α and β are two constants that can be found from the initial conditions.

This still describes the curve y(x), the solution to the brachistochrone problem, perfectly well – it’s just that we cannot solve these equations to get an expression directly for y in terms of x. We can only describe the coordinates of the curve y(x) “implicitly” in terms of a curve parameter θ.

Now, in terms of how to actually interpret what this solution means, it turns out that the equations above describe a well-known geometric object called a cycloid. A general cycloid curve is basically formed by drawing a circle and a point on the circumference of the circle and then letting this circle “roll” along the x-axis:

This means that our solution to the brachistochrone problem or in other words, the curve of shortest rolling time between two points, is given by the arc of a cycloid curve. More precisely, the curve that is the actual solution to our problem is given by the arc of an inverted cycloid:

Solution of The Brachistochrone Using The Beltrami Identity

So, we have our integrand function f as:

We can now simply plug this into the Beltrami identity:

This will give us a differential equation we can hopefully solve to find the curve y(x) that minimizes the rolling time of the cart. First, let’s calculate this partial derivative (note that the denominator does not involve y’, so it can be pulled outside the derivative):

\frac{\partial f}{\partial y'}=\frac{\partial}{\partial y'}\left(\sqrt{\frac{m}{2E}}\sqrt{\frac{1+y'^2}{1-\frac{mg}{E}y}}\right)=\sqrt{\frac{m}{2E}}\frac{1}{\sqrt{1-\frac{mg}{E}y}}\frac{\partial}{\partial y'}\left(\sqrt{1+y'^2}\right)

Using the power rule and the chain rule here, we get:

\frac{\partial f}{\partial y'}=\sqrt{\frac{m}{2E}}\frac{1}{\sqrt{1-\frac{mg}{E}y}}\frac{1}{2\sqrt{1+y'^2}}\cdot\frac{\partial}{\partial y'}\left(1+y'^2\right)

=\sqrt{\frac{m}{2E}}\frac{1}{\sqrt{1-\frac{mg}{E}y}}\frac{1}{2\sqrt{1+y'^2}}\cdot2y'

=\sqrt{\frac{m}{2E}}\frac{y'}{\sqrt{1-\frac{mg}{E}y}\sqrt{1+y'^2}}

Now, let’s plug this expression (and the expression for f itself) into the Beltrami identity to get:

\frac{\partial f}{\partial y'}y'-f=C\ \ \Rightarrow\ \ \sqrt{\frac{m}{2E}}\frac{y'}{\sqrt{1-\frac{mg}{E}y}\sqrt{1+y'^2}}y'-\sqrt{\frac{m}{2E}}\sqrt{\frac{1+y'^2}{1-\frac{mg}{E}y}}=C

Let’s divide both sides first by (m/2E)^1/2 and then multiply by (1-mgy/E)^1/2 to get:

\frac{y'^2}{\sqrt{1+y'^2}}-\sqrt{1+y'^2}=C\sqrt{\frac{2E}{m}}\sqrt{1-\frac{mg}{E}y}

Moreover, let’s multiply both sides by (1+y’²)^1/2:

y'^2-\left(\sqrt{1+y'^2}\right)^2=C\sqrt{\frac{2E}{m}}\sqrt{1-\frac{mg}{E}y}\sqrt{1+y'^2}

\Rightarrow\ \ y'^2-\left(1+y'^2\right)=C\sqrt{\frac{2E}{m}}\sqrt{1-\frac{mg}{E}y}\sqrt{1+y'^2}

\Rightarrow\ \ -1=C\sqrt{\frac{2E}{m}}\sqrt{1-\frac{mg}{E}y}\sqrt{1+y'^2}

\Rightarrow\ \ -\frac{1}{C}\sqrt{\frac{m}{2E}}=\sqrt{1-\frac{mg}{E}y}\sqrt{1+y'^2}

Next, let’s square both sides, multiply out the parentheses on the right-hand side and solve for y’²:

\frac{m}{2EC^2}=\left(1-\frac{mg}{E}y\right)\left(1+y'^2\right)

\Rightarrow\ \ \frac{m}{2EC^2}=1-\frac{mg}{E}y+y'^2-\frac{mg}{E}yy'^2

\Rightarrow\ \ \frac{m}{2EC^2}-1=-\frac{mg}{E}\left(y-\left(\frac{E}{mg}-y\right)y'^2\right)

\Rightarrow\ \ \frac{E}{mg}-\frac{1}{2gC^2}=y-\left(\frac{E}{mg}-y\right)y'^2

\Rightarrow\ \ \frac{-\frac{E}{mg}+\frac{1}{2gC^2}+y}{\frac{E}{mg}-y}=y'^2

We can now take the square root of both sides and write y’=dy/dx:

\frac{dy}{dx}=\sqrt{\frac{\frac{1}{2gC^2}-\left(\frac{E}{mg}-y\right)}{\frac{E}{mg}-y}}

This differential equation is now in a form we can integrate and solve. We’ll begin doing so by defining some new constants (just to simplify things), α=1/2gC² and β=E/mg, such that we now have:

\frac{dy}{dx}=\sqrt{\frac{\alpha-\left(\beta-y\right)}{\beta-y}}

Then, let’s multiply by dx, divide by the expression on the right-hand side (this “technique” is called separation of variables – we move everything involving x’s to one side and everything involving y’s to the other side) and integrate both sides. Doing these steps, we have:

\int_{ }^{ }\sqrt{\frac{\beta-y}{\alpha-\left(\beta-y\right)}}dy=\int_{ }^{ }dx

On the right-hand side, we simply get x+A (with A being some integration constant). The integral on the left, however, is quite tough but we can still solve it in a way with a few substitutions.

First, let’s make the substitution u = β – y. If we do this, the integration measure du would now be du = -dy, in which case the integral on the left-hand side turns into:

\int_{ }^{ }\sqrt{\frac{\beta-y}{\alpha-\left(\beta-y\right)}}dy\ \ \Rightarrow\ \ -\int_{ }^{ }\sqrt{\frac{u}{\alpha-u}}du

Now we’ll factor out α from inside the square root:

-\int_{ }^{ }\sqrt{\frac{u}{\alpha\left(1-\frac{u}{\alpha}\right)}}du=-\frac{1}{\sqrt{\alpha}}\int_{ }^{ }\sqrt{\frac{u}{1-\frac{u}{\alpha}}}du

We can then do another substitution of the form sin²θ = u/α. The integration measure du would then become (by differentiating both sides):

2\sin\theta\cos\theta d\theta=\frac{du}{\alpha}\ \ \Rightarrow\ \ du=2\alpha\sin\theta\cos\theta d\theta

With these, our integral becomes:

-\frac{1}{\sqrt{\alpha}}\int_{ }^{ }\sqrt{\frac{u}{1-\frac{u}{\alpha}}}du\ \ \Rightarrow\ \ -\frac{1}{\sqrt{\alpha}}\int_{ }^{ }\sqrt{\frac{\alpha\sin^2\theta}{1-\sin^2\theta}}\cdot2\alpha\sin\theta\cos\theta d\theta

We can use the trigonometric identity 1 – sin²θ = cos²θ here to get:

-\frac{1}{\sqrt{\alpha}}\int_{ }^{ }\sqrt{\frac{\alpha\sin^2\theta}{\cos^2\theta}}\cdot2\alpha\sin\theta\cos\theta d\theta

=-\frac{1}{\sqrt{\alpha}}\int_{ }^{ }\frac{\sqrt{\alpha}\sin\theta}{\cos\theta}\cdot2\alpha\sin\theta\cos\theta d\theta

=-2\alpha\int_{ }^{ }\sin^2\theta d\theta

This is now a fairly simple integral to do, which you’ll find the solution to in practically any integration table (or just look up the techniques on how to do it – for example, this Youtube video shows it quite well. In any case, the solution you’ll get is:

-2\alpha\int_{ }^{ }\sin^2\theta d\theta=-2\alpha\left(\frac{1}{2}\theta-\frac{1}{4}\sin2\theta\right)=-\alpha\theta+\frac{\alpha}{2}\sin2\theta

Note that we don’t have to add an integration constant here because we already added one on the right-hand side of our original equation, which now becomes:

\int_{ }^{ }\sqrt{\frac{\beta-y}{\alpha-\left(\beta-y\right)}}dy=\int_{ }^{ }dx\ \ \Rightarrow\ \ -\alpha\theta+\frac{\alpha}{2}\sin2\theta=x+A

We can solve this to get an expression for x in terms of the parameter θ:

x=\alpha\left(\frac{1}{2}\sin2\theta-\theta\right)-A

Now, we know from our earlier substitutions that u = αsin²θ and also that u = β – y (these were the substitutions we did to solve the integral). From these, we can solve for y in terms of the parameter θ:

In this case, it’s not really possible to solve for y in terms of x from these equations directly, so it’s worthwhile to just leave this equation in terms of this parameter θ. We then have two parametric equations describing the solution of the brachistochrone curve:

We’ll set this constant A=0 (since it corresponds to the value of x at θ=0, which we can simply set to be at the origin). Finally, just to make these expressions look prettier, let’s rescale the value of θ to θ/2 to get:

Solution of The Brachistochrone Using The Euler-Lagrange Equation

Here, we will find the solution to the brachistochrone problem using the Euler-Lagrange equation instead of the Beltrami identity like we did in before. This will illustrate the fact that both lead to the exact same result, but with different levels of complexity (the Beltrami identity turns out to be MUCH simpler).

Now, the Euler-Lagrange equations state that for us to minimize the rolling time, i.e. the function f, we need to plug it into the following equation:

\frac{d}{dx}\frac{\partial f}{\partial y'}-\frac{\partial f}{\partial y}=0\ {,}\ \ f=\sqrt{\frac{m}{2E}}\sqrt{\frac{1+y'^2}{1-\frac{mg}{E}y}}

So, let’s do exactly that! First, let’s calculate the derivative ∂f/∂y:

\frac{\partial f}{\partial y}=\frac{\partial}{\partial y}\left(\sqrt{\frac{m}{2E}}\sqrt{\frac{1+y'^2}{1-\frac{mg}{E}y}}\right)

=\sqrt{\frac{m}{2E}}\sqrt{1+y'^2}\frac{\partial}{\partial y}\left(1-\frac{mg}{E}y\right)^{-\frac{1}{2}}

=\sqrt{\frac{m}{2E}}\sqrt{1+y'^2}\cdot\left(-\frac{1}{2}\right)\left(1-\frac{mg}{E}y\right)^{-\frac{3}{2}}\cdot\frac{\partial}{\partial y}\left(1-\frac{mg}{E}y\right)

=\sqrt{\frac{m}{2E}}\sqrt{1+y'^2}\cdot\left(-\frac{1}{2}\right)\left(1-\frac{mg}{E}y\right)^{-\frac{3}{2}}\cdot\left(-\frac{mg}{E}\right)

=\sqrt{\frac{m}{2E}}\frac{mg}{2E}\frac{\sqrt{1+y'^2}}{\left(1-\frac{mg}{E}y\right)\sqrt{1-\frac{mg}{E}y}}

Now, we already calculated ∂f/∂y’ previously, so let’s use that here. As a reminder, the result was:

\frac{\partial f}{\partial y'}=\sqrt{\frac{m}{2E}}\frac{y'}{\sqrt{1-\frac{mg}{E}y}\sqrt{1+y'^2}}

Finally, we need to take the derivative of this expression, i.e. calculate d/dx(∂f/∂y’) (note that both y and y’ here depend on x, so we have to use the product and chain rules):

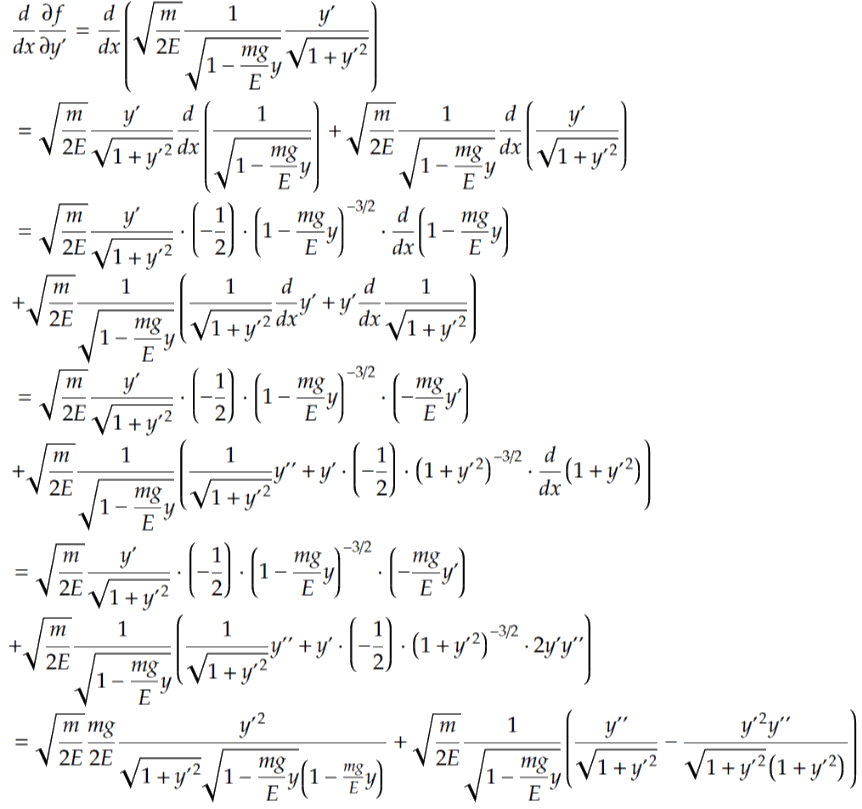
This is a somewhat terrifying looking expression. However, we can clean it up a little by first writing out the parentheses in the second term and then factoring out some common terms. Doing that, we get:

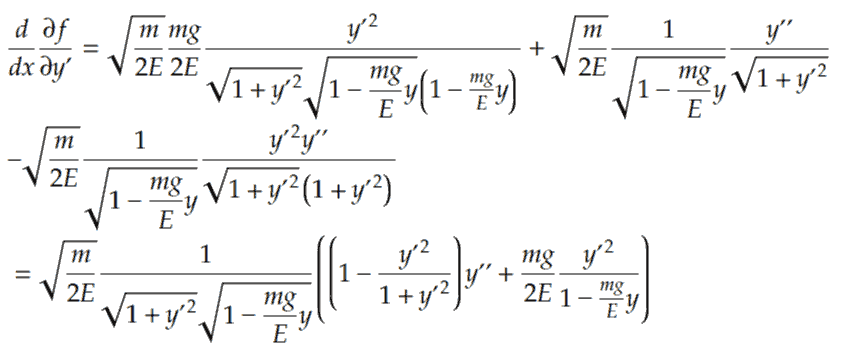
If we now combine both of the expressions we’ve obtained into the Euler-Lagrange equation (so both d/dx(∂f/∂y’) and ∂f/∂y), we have:

\Rightarrow\ \ \sqrt{\frac{m}{2E}}\frac{1}{\sqrt{1+y'^2}\sqrt{1-\frac{mg}{E}y}}\left(\left(1-\frac{y'^2}{1+y'^2}\right)y''+\frac{mg}{2E}\frac{y'^2}{1-\frac{mg}{E}y}\right)-\sqrt{\frac{m}{2E}}\frac{mg}{2E}\frac{\sqrt{1+y'^2}}{\left(1-\frac{mg}{E}y\right)\sqrt{1-\frac{mg}{E}y}}=0

We can immediately multiply to get rid of the common denominator (1-mgy/E)^1/2 and also divide out the common factor (m/2E)^1/2. We then have:

\frac{1}{\sqrt{1+y'^2}}\left(\left(1-\frac{y'^2}{1+y'^2}\right)y''+\frac{mg}{2E}\frac{y'^2}{1-\frac{mg}{E}y}\right)-\frac{mg}{2E}\frac{\sqrt{1+y'^2}}{\left(1-\frac{mg}{E}y\right)}=0

Then, let’s multiply by (1+y’²)^1/2 to get:

\left(1-\frac{y'^2}{1+y'^2}\right)y''+\frac{mg}{2E}\frac{y'^2}{1-\frac{mg}{E}y}-\frac{mg}{2E}\frac{1+y'^2}{1-\frac{mg}{E}y}=0

We can factor the second and third terms and write them as follows:

\left(1-\frac{y'^2}{1+y'^2}\right)y''+\frac{mg}{2E}\frac{1}{1-\frac{mg}{E}y}\left(y'^2-\left(1+y'^2\right)\right)=0

\Rightarrow\ \ \left(1-\frac{y'^2}{1+y'^2}\right)y''-\frac{mg}{2E}\frac{1}{1-\frac{mg}{E}y}=0

Let’s multiply all terms by 1+y’² to get:

\left(1+y'^2\right)\left(1-\frac{y'^2}{1+y'^2}\right)y''-\frac{mg}{2E}\frac{1+y'^2}{1-\frac{mg}{E}y}=0

\Rightarrow\ \ \left(1+y'^2-\left(1+y'^2\right)\frac{y'^2}{1+y'^2}\right)y''-\frac{mg}{2E}\frac{1+y'^2}{1-\frac{mg}{E}y}=0

\Rightarrow\ \ y''-\frac{mg}{2E}\frac{1+y'^2}{1-\frac{mg}{E}y}=0

\Rightarrow\ \ y''=\frac{mg}{2E}\frac{1+y'^2}{1-\frac{mg}{E}y}

It turns out that this is actually the same differential equation we would obtain from the Beltrami identity, however, it is certainly not obvious just from looking at this – we need to manipulate this into the right form (and also integrate once) to see it. First, let’s multiply everything by 2y’:

2y'y''=\frac{mg}{E}\frac{1+y'^2}{1-\frac{mg}{E}y}y'

On the left-hand side, if you think about it for a while, this is just the chain rule applied to y’²:

We can therefore insert this to the left-hand side and then divide everything by 1+y’²:

\frac{d}{dx}y'^2=\frac{mg}{E}\frac{1+y'^2}{1-\frac{mg}{E}y}y'\ \ \Rightarrow\ \ \frac{1}{1+y'^2}\frac{d}{dx}y'^2=\frac{mg}{E}\frac{1}{1-\frac{mg}{E}y}y'

If you stare at this for a while, you might notice that the right-hand side is also in the form of the chain rule applied to an expression – in particular, to the expression ln(1-mgy/E). This is because:

\frac{d}{dx}\ln\left(1-\frac{mg}{E}y\right)=\frac{1}{1-\frac{mg}{E}y}\frac{d}{dx}\left(1-\frac{mg}{E}y\right)=\frac{1}{1-\frac{mg}{E}y}\left(-\frac{mg}{E}y'\right)

This is exactly what we have on the right-hand side (apart from a minus sign). We can therefore write:

\frac{1}{1+y'^2}\frac{d}{dx}y'^2=\frac{mg}{E}\frac{1}{1-\frac{mg}{E}y}y'

\Rightarrow\ \ \frac{1}{1+y'^2}\frac{d}{dx}y'^2=-\frac{d}{dx}\ln\left(1-\frac{mg}{E}y\right)

This is now in a nice form to be integrated. So, integrating both sides with respect to x, we have:

\int_{ }^{ }\frac{1}{1+y'^2}\frac{d}{dx}y'^2dx=-\int_{ }^{ }\frac{d}{dx}\ln\left(1-\frac{mg}{E}y\right)dx

On the right-hand side, the integral and derivative “cancel” one another and we just get the ln-expression back (as well as an integration constant, which I’ll label A here):

\int_{ }^{ }\frac{1}{1+y'^2}\frac{d}{dx}y'^2dx=-\ln\left(1-\frac{mg}{E}y\right)+A

On the left-hand side, we can do a change of variables with u=1+y’², such that:

du=\frac{du}{dx}dx=\frac{d}{dx}\left(1+y'^2\right)dx=\frac{d}{dx}y'^2dx

The above equation would then become:

\Rightarrow\ \ \int_{ }^{ }\frac{1}{u}du=-\ln\left(1-\frac{mg}{E}y\right)+A

\Rightarrow\ \ \ln u=-\ln\left(1-\frac{mg}{E}y\right)+A — Here, I’ve simply used the fact that the integral of 1/u is ln|u| and since u=1+y’² is always positive, we can drop the absolute value signs.

We therefore have:

\ln\left(1+y'^2\right)=-\ln\left(1-\frac{mg}{E}y\right)+A

A nice property of logarithms is that we can bring the multiplicative factor -1 in front of the logarithm to become an exponent inside, in other words:

\Rightarrow\ \ \ln\left(1+y'^2\right)=\ln\left(\left(1-\frac{mg}{E}y\right)^{-1}\right)+A

\Rightarrow\ \ \ln\left(1+y'^2\right)=\ln\left(\frac{1}{1-\frac{mg}{E}y}\right)+A

Now, since the constant A is arbitrary, we might as well write it as the logarithm of some other arbitrary constant B, i.e. as A=ln(B) . This allows us to use the property of logarithms that for any two numbers x₁ and x₂, ln(x₁)+ln(x₁)=ln(x₁x₂), meaning that:

\ln\left(1+y'^2\right)=\ln\left(\frac{1}{1-\frac{mg}{E}y}\right)+\ln B\ \ \Rightarrow\ \ \ln\left(1+y'^2\right)=\ln\left(B\frac{1}{1-\frac{mg}{E}y}\right)

Here we have two logarithms equal to one another – this means that whatever is inside the logarithms must also be equal (assuming they both have the same domains here). We therefore have:

Let’s factor out mg/E from the denominator on the right and also subtract 1 from both sides. Doing this, we have:

y'^2=B\frac{1}{\frac{mg}{E}\left(\frac{E}{mg}-y\right)}-1\ \ \Rightarrow\ \ y'^2=\frac{\frac{BE}{mg}}{\frac{E}{mg}-y}-1

Now, we can also express 1 as:

With this, we then have:

y'^2=\frac{\frac{BE}{mg}}{\frac{E}{mg}-y}-\frac{\frac{E}{mg}-y}{\frac{E}{mg}-y}\ \ \Rightarrow\ \ y'^2=\frac{\frac{BE}{mg}-\left(\frac{E}{mg}-y\right)}{\frac{E}{mg}-y}

Since B here is again arbitrary, we can simply define it in terms of some other constant C as B=m/2EC². Doing this and taking the square root on both sides, we have:

y'=\sqrt{\frac{\frac{m}{2EC^2}\frac{E}{mg}-\left(\frac{E}{mg}-y\right)}{\frac{E}{mg}-y}}

\Rightarrow\ \ \frac{dy}{dx}=\sqrt{\frac{\frac{1}{2gC^2}-\left(\frac{E}{mg}-y\right)}{\frac{E}{mg}-y}}

This is now the exact same differential equation for the brachistochrone problem we found from the Beltrami identity and therefore, has the same solutions as well (which we already found before).

Now, this highlights an important point – as you can see, the calculations we had to do using the Euler-Lagrange equation were MUCH more complicated than by using the Beltrami identity to get the exact same result.

This highlights the fact that in many cases, the Beltrami identity can greatly simplify calculations compared to using the Euler-Lagrange equation, which shows why it is useful.

However, you just have to keep in mind that the Beltrami identity is not necessarily valid in all problems (namely, in problems where ∂f/∂x≠0), while the Euler-Lagrange equation is.

Optics

Surprisingly, variational calculus is an incredibly important tool used in the field of optics. Optics is the area of physics concerned with the behaviour of light (electromagnetic radiation) and how light interacts with matter.

A full treatment of how light interacts with matter would require quantum electrodynamics. However, classical and geometrical optics (what we’re going to briefly talk about here) still has an incredible number of technological applications, such as designing mirrors, microscopes, lenses and things like that.

We’ll begin by talking about something known as Fermat’s principle and derive one of the most famous results in geometrical optics called Snell’s law. Then, we’ll look at how to predict the motion of light rays in a material using Fermat’s principle – of course, all of this will be done using the tools of variational calculus.

Fermat’s Principle & Snell’s Law

Here, we’re going to discuss one of the most foundational principles in optics known as Fermat’s principle. Essentially, Fermat’s principle determines how all light rays move (classically, that is – we’re not accounting for any quantum stuff here), either in a vacuum or in some sort of material (or through several materials).

The statement of Fermat’s principle is actually quite simple:

“The path taken by a light ray between any two points is the path that minimizes the travel time between the points.”

So, if we want to find the path of a given light ray between two points, according to Fermat’s principle, we simply have to find the path along which the light ray takes the least amount of time to travel between the two points.

This lends itself perfectly to be a calculus of variations problem. This is because the travel time of a light ray will often be described by a functional. Actually, we already was a somewhat different example of this – the brachistochrone problem.

As a sidenote, Fermat’s principle technically states that the time taken by a light ray should be stationary – that is, either a minimum, a maximum or just a stationary solution. However, in the language of variational calculus, there isn’t really much difference between these three different types of stationary solutions and they are all calculated the same way (from the Euler-Lagrange equations).

So, for all practical purposes, it doesn’t matter whether we talk about minima or just stationary solutions in general. These are all obtained in exactly the same way and we’re not going to be distinguishing between these – I simply wanted to mention this as a technical detail.

So, from Fermat’s principle and by applying calculus of variations, we can essentially derive how light rays behave, for example, at a boundary between two materials. The law we get as a result of Fermat’s principle and calculus of variations for this case is known as Snell’s law:

\frac{\sin\theta_1}{\sin\theta_2}=\frac{n_2}{n_1}

This equation states that the ratio of the sines of the incidence angle θ₁ and the refraction angle θ₂ is inversely proportional to the ratio of the refractive indices of the two materials the light ray passes through:

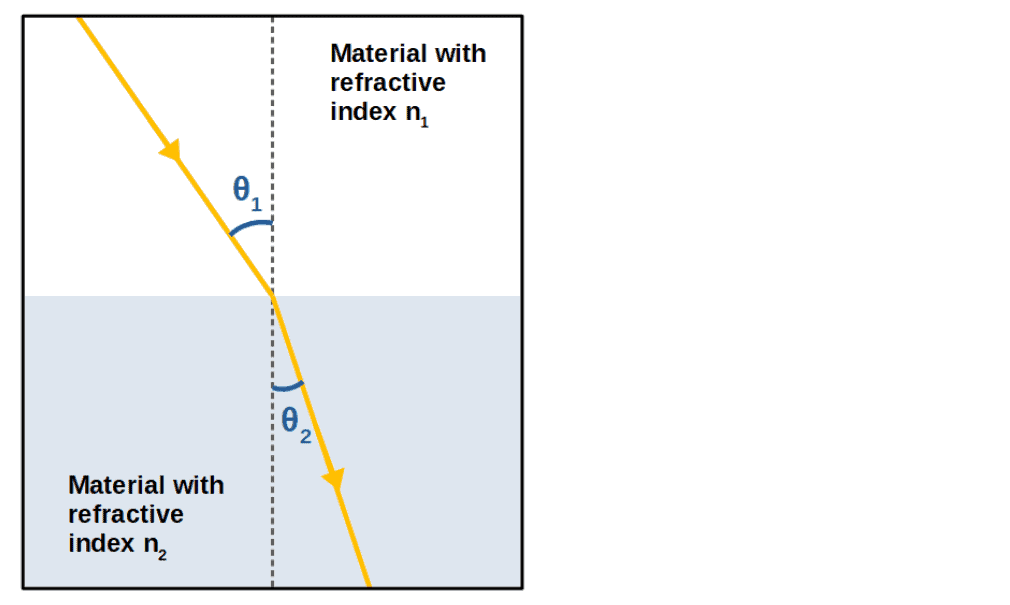
Essentially, Snell’s law dictates the behaviour of a light ray passing through a boundary of two materials. The important thing is that Snell’s law is simply a consequence of Fermat’s principle and we can derive it using variational calculus (you’ll see this done below).

Derivation of Snell's Law From Fermat's Principle

The setup here is that we have two materials with refractive indices n₁ and n₂. The refractive index simply describes what the speed of a light ray will be in a given material, given by v=c/n.

We’re going to place the whole system in an x,y -coordinate system with the boundary of the materials at y=0. The whole trajectory of a light ray between the points a and b is then given by some curve y(x):

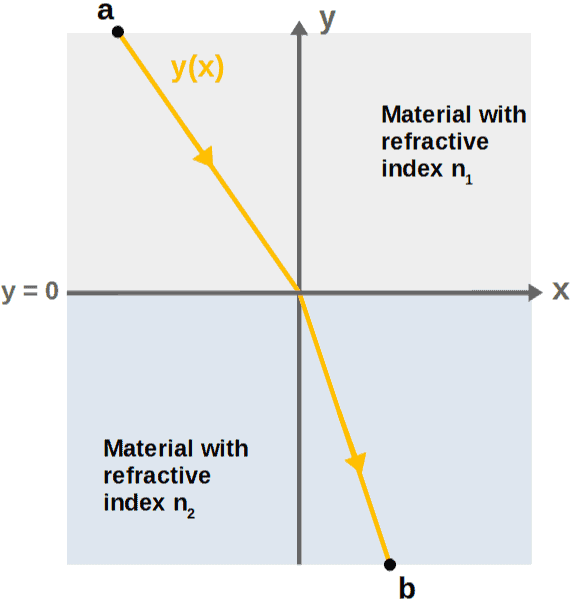
We can again break up the path y(x) into small pieces with length ds = (dx² + dy²)^1/2 just like we’ve done in all the previous examples. It then takes a time dt=ds/v, where v is the speed, for the light ray to travel each of these small distance pieces.

The total time for the light ray to move from a to b is then given by integrating these small dt-time intervals:

T=\int_a^bdt=\int_a^b\frac{ds}{v}=\int_a^b\frac{\sqrt{dx^2+dy^2}}{v}=\int_a^b\frac{\sqrt{1+y'^2}}{v}dx

Here, I’ve again pulled out dx² from inside the square root to get y’=dy/dx.

Now, the key here is to realize that the speed of the light ray, v , is actually a function of the vertical distance along the path, y(x). This is because the speed of the light ray changes when the ray moves from the first material to the second material.

Generally, we can calculate the speed of light inside a material by dividing c (speed of light in a vacuum) by the refractive index of the material. In our case, this would be a function of y:

v\left(y\right)=\frac{c}{n\left(y\right)}

The speed of the light ray in the n₁-material is v₁=c/n₁ and v₂=c/n₂ in the n₂-material, likewise. We can then express the speed as a piecewise function of y:

v\left(y\right)=\frac{c}{n\left(y\right)}=\begin{cases}
\frac{c}{n_1}&{,}\ y\gt 0\\
\frac{c}{n_2}&{,}\ y\lt 0
\end{cases}

Here, we’re essentially thinking of n(y) as a piecewise functio of y (this makes sense because n does change with y as we move from one material to the other – it just changes at one point only):

n\left(y\right)=\begin{cases}
n_1&{,}\ y\gt 0\\
n_2&{,}\ y\lt 0
\end{cases}

Our total time functional then becomes:

T=\int_a^b\frac{\sqrt{1+y'^2}}{v}dx\ \ \Rightarrow\ \ T=\int_a^b\frac{n\left(y\right)}{c}\sqrt{1+y'^2}dx

Now, let’s see what we get by minimizing this functional (this will give us the paths of minimum travel time between a and b). If you notice, the integrand here is independent of x (explicitly – of course, y and y’ still implicitly depend on x), so we can use the Beltrami identity:

Plugging the integrand f into this, we get:

\frac{\partial}{\partial y'}\left(\frac{n\left(y\right)}{c}\sqrt{1+y'^2}\right)y'-\frac{n\left(y\right)}{c}\sqrt{1+y'^2}=C

\Rightarrow\ \ \frac{n\left(y\right)}{c}\left(\frac{1}{2\sqrt{1+y'^2}}\cdot\frac{\partial}{\partial y'}\left(1+y'^2\right)\right)y'-\frac{n\left(y\right)}{c}\sqrt{1+y'^2}=C

\Rightarrow\ \ \frac{n\left(y\right)}{c}\frac{y'^2}{\sqrt{1+y'^2}}-\frac{n\left(y\right)}{c}\sqrt{1+y'^2}=C

Multiplying by c/n(y) and also by (1+y’²)^1/2, we get:

y'^2-\left(\sqrt{1+y'^2}\right)^2=\frac{Cc}{n\left(y\right)}\sqrt{1+y'^2}

\Rightarrow\ \ -1=\frac{Cc}{n\left(y\right)}\sqrt{1+y'^2}

Instead of just solving for y(x) from this (which would give us the equation for a straight line), we can do something clever. Let’s first write this in the form:

-\frac{n\left(y\right)}{Cc}=\sqrt{1+y'^2}=\sqrt{1+\left(\frac{dy}{dx}\right)^2}

Now, let’s pull out 1/dx² from inside the square root as follows:

-\frac{n\left(y\right)}{Cc}=\sqrt{\frac{1}{dx^2}\left(dx^2+dy^2\right)}

\Rightarrow\ \ -\frac{n\left(y\right)}{Cc}=\frac{\sqrt{dx^2+dy^2}}{dx}=\frac{ds}{dx}

As a reminder, this distance piece ds corresponds to a small distance along the path of the light ray. Looking at the picture from above, we can do a little trigonometry and get another expression for ds/dx:

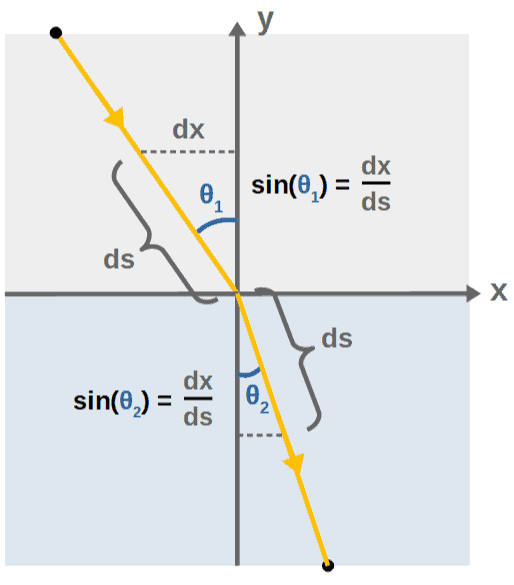
So, depending on which side side of y=0 (in which material) the light ray is, we either have dx/ds=sin(θ₁) or dx/ds=sin(θ₂). We could express this using a piecewise function as well:

\frac{dx}{ds}=\sin\theta\left(y\right)\ {,}\ \ \ \theta\left(y\right)=\begin{cases}
\theta_1&{,}\ y\gt 0\\
\theta_2&{,}\ y\lt 0
\end{cases}

Now, inserting dx/ds=sinθ(y) into our equation from above, we have:

-\frac{n\left(y\right)}{Cc}=\frac{ds}{dx}

\Rightarrow\ \ -\frac{n\left(y\right)}{Cc}=\frac{1}{\sin\theta\left(y\right)}

\Rightarrow\ \ -Cc=n\left(y\right)\sin\theta\left(y\right)

We really have two equations here, depending on whether y>0 or y<0:

\begin{cases}
-Cc=n_1\sin\theta_1&{,}\ y\gt 0\\
-Cc=n_2\sin\theta_2&{,}\ y\lt 0
\end{cases}

The important thing is that these are both equal to the same constant -cC. Therefore, we can equate these two expressions and get:

\Rightarrow\ \ \frac{\sin\theta_1}{\sin\theta_2}=\frac{n_2}{n_1}

This is, of course, nothing but Snell’s law! The key point with all of this is that Snell’s law is just a consequence of Fermat’s principle, which we were able to derive using calculus of variations.

Snell’s Law & Trajectories of Light

Now, Snell’s law only applies to light passing through a boundary between two isotropic materials. These are essentially materials in which the refractive index (n) is approximately constant everywhere, like glass or air.

However, we can also have materials in which the refractive index varies inside the material. Generally, this would make the refractive index a function of position, n(x,y,z). These types of materials are called anisotropic.

A light ray moving in an anisotropic material behaves very differently than a light ray moving in an isotropic material (in which case the rays just move in straight lines dictated by Snell’s law, as we saw before).

The nice thing is that Fermat’s principle still applies for a light ray moving in an anisotropic material – the ray will move such that its travel time between two points is minimized. We can therefore derive the trajectory of a light ray in an anisotropic material the same way as we did above with Snell’s law!

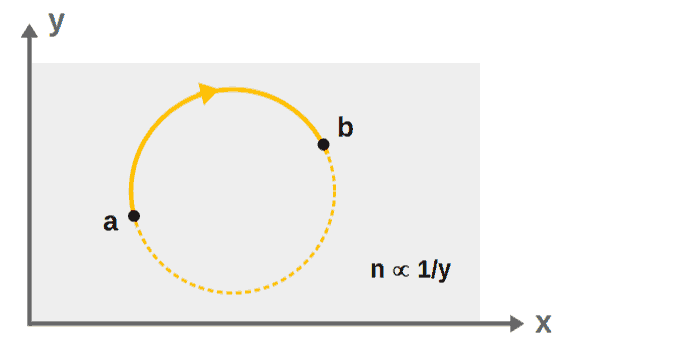
Below, I’ve included an interesting example of this – in this example, we see that in an anisotropic material with refractive index inversely proportional to the vertical distance inside the material, a light ray will actually move along a circular arc.

Example: Circular Trajectories of Light In an Anisotropic Medium

Let’s go back to the travel time functional from the previous example (derivation of Snell’s law):

T=\int_a^b\frac{n\left(y\right)}{c}\sqrt{1+y'^2}dx

Here, we haven’t specified what this refractive index n(y) is yet. This functional therefore applies to any curve y(x) inside any material with a refractive index that depends on the y-coordinate only.

The setup in this example will be as follows; we have some material in which the refractive index varies in the vertical direction (the y-direction) as:

n\left(y\right)=\frac{L}{y} — This L here is a constant corresponding to the length of the material block.

We then want to find the path a light ray would move along from some point a to another point b inside of this material:

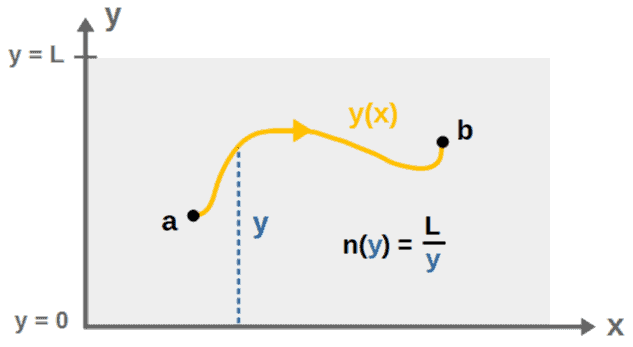
The functional describing the travel time for the light ray between a and b is, in this case:

To find the curve y(x) that minimizes this functional, we can again apply the Beltrami identity to the integrand f here:

\Rightarrow\ \ \frac{\partial}{\partial y'}\left(\frac{L}{cy}\sqrt{1+y'^2}\right)y'-\frac{L}{cy}\sqrt{1+y'^2}=C

\Rightarrow\ \ \frac{L}{cy}\frac{y'^2}{\sqrt{1+y'^2}}-\frac{L}{cy}\sqrt{1+y'^2}=C

\Rightarrow\ \ \frac{L}{cy}y'^2-\frac{L}{cy}\left(1+y'^2\right)=C\sqrt{1+y'^2}

\Rightarrow\ \ -1=\frac{Cc}{L}y\sqrt{1+y'^2}

Now, squaring both sides and solving for y’=dy/dx, we get:

\frac{dy}{dx}=\sqrt{\frac{L^2}{C^2c^2y^2}-1}

We can factor out L²/C²c²y² from inside the square root and get:

\frac{dy}{dx}=\sqrt{\frac{L^2}{C^2c^2y^2}\left(1-\frac{C^2c^2y^2}{L^2}\right)}=\frac{L}{Cc}\frac{\sqrt{1-\frac{C^2c^2y^2}{L^2}}}{y}

Now, dividing so that we have all the y-stuff on the left-hand side and then integrating, we get:

\frac{y}{\sqrt{1-\frac{C^2c^2y^2}{L^2}}}\frac{dy}{dx}=\frac{L}{Cc}

\Rightarrow\ \ \int_{ }^{ }\frac{y}{\sqrt{1-\frac{C^2c^2y^2}{L^2}}}dy=\int_{ }^{ }\frac{L}{Cc}dx

\Rightarrow\ \ \int_{ }^{ }\frac{y}{\sqrt{1-\frac{C^2c^2y^2}{L^2}}}dy=\frac{L}{Cc}x+A — This A here is an integration constant.

Now, we can solve this integral on the left quite easily by doing a substitution of the form u = 1 – C²c²y²/L, in which case we we’d have:

du=\frac{du}{dy}dy=du=\frac{d}{dy}\left(1-\frac{C^2c^2y^2}{L^2}\right)dy=-\frac{2C^2c^2}{L^2}ydy\ \ \Rightarrow\ \ dy=-\frac{L^2}{2C^2c^2}\frac{du}{y}

Doing this, the integral becomes:

\int_{ }^{ }\frac{y}{\sqrt{1-\frac{C^2c^2y^2}{L^2}}}dy

\Rightarrow\ \ \int_{ }^{ }\frac{y}{\sqrt{u}}\left(-\frac{L^2}{2C^2c^2}\frac{du}{y}\right)

=-\frac{L^2}{2C^2c^2}\int_{ }^{ }\frac{1}{\sqrt{u}}du

=-\frac{L^2}{C^2c^2}\sqrt{1-\frac{C^2c^2y^2}{L^2}} — Here I’ve simply substituted back in the definition of u in terms of y.

So, all in all, we then have the following equation:

-\frac{L^2}{C^2c^2}\sqrt{1-\frac{C^2c^2y^2}{L^2}}=\frac{L}{Cc}x+A

Let’s multiply by c²C²/L² and square both sides to get:

-\sqrt{1-\frac{C^2c^2y^2}{L^2}}=\frac{Cc}{L}x+\frac{C^2c^2A}{L^2}

\Rightarrow\ \ 1-\frac{C^2c^2y^2}{L^2}=\left(\frac{Cc}{L}x+\frac{C^2c^2A}{L^2}\right)^2

\Rightarrow\ \ y^2+\left(x+\frac{CcA}{L}\right)^2=\frac{L^2}{C^2c^2}

For last, we can make this equation prettier by defining the following new constants:

r^2=\frac{L^2}{C^2c^2}\ {,}\ \ x_0=-\frac{CcA}{L}

We would then have:

Can you see what this equation describes? This is the equation for a circle of radius r! In this case, it would actually be a circle centered at (x₀,0).

So, we’ve arrived at the result that in a material with refractive index n∝1/y, light rays travel along circular trajectories (or along circular arcs):

Vector Calculus For Physics: A Complete Self-Study Course