Functionals & Variations

In this part of the course, we will be diving into an area of math that shows up everywhere in advanced physics – calculus of variations.

Everything discussed in this part of the course is going to build on top of the things we’ve covered previously, such as single- and multivariable calculus.

Everything we cover is also going to be quite physics-biased with lots of physical examples and applications, so this is not going to be the most rigorous introduction to calculus of variations. The goal is to give you the tools you’ll need to understand physics first and foremost and what we learn here will certainly be sufficient for that.

In this lesson, we will first begin by going over the underlying goal of what calculus of variations is all about as well as some of the basic concepts.

In later chapters, we will be going over lots of applications, examples and overall, looking at variational calculus at a deeper level. Throughout the lessons, we will also discover lots of ways in which variational calculus appears in our current description of modern physics.

Lesson Contents

Brief Introduction To Calculus of Variations

At this point, we’ve briefly touched on minimizing or maximizing single-variable functions (such as in some of the exercises). The applications of finding minima or maxima of single-variable functions are not very difficult to figure out.

We might, for example, have a function that describes the current in an electric circuit as a function of time and finding the maxima of this function would equate to knowing when the current is the biggest – lots of real-world applications with that one!

Essentially, if we have a function of some variable, f(x), we find its extremal points (either minima, maxima or stationary points in general) by setting its first derivative equal to zero, df/dx=0 and solving for the value of x.

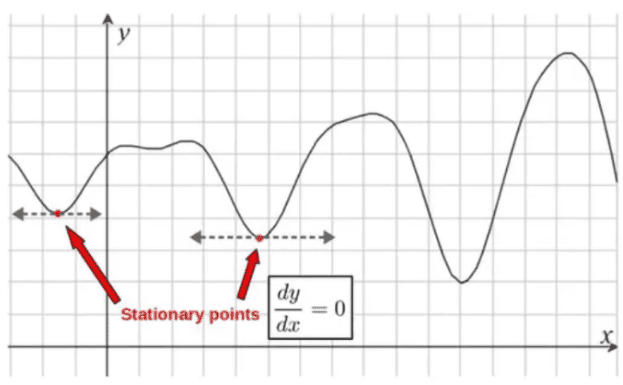
This gives us the value of the variable x at which the function is at an extremal point, in other words, when the function f(x) has a minimum, maximum or stationary value.

The underlying reasoning for why we want to solve the equation df(x)/dx=0 specifically comes from the fact that the slope of the tangent line of a given function (described by the derivative of that function) is zero at the stationary points.

Example: Finding The Minimum of a Radial Potential Energy Function

A very common physical application of finding extrema of single-variable functions is for finding the minimum of an “effective potential”.

In general, an effective potential function for a particle of mass m in some central potential V(r) (meaning that the potential, or the force acting on the particle, only depends on the radial distance to the center – for example, gravitational potentials are of this form) has the form:

V_{eff}\left(r\right)=\frac{L^2}{2mr^2}+V\left(r\right) — Here, L is the angular momentum of the particle and it is a constant (i.e. conserved).

The effective potential is an extremely useful tool for qualitative analysis of how a given system behaves. For example, by plotting the effective potential, we can literally see how a system will behave.

The reason we often analyze effective potentials in many problems involving rotation in 3D is because the effective potential nicely incorporates both of the “radial” as well as the “angular” motion of a system.

The first term in the effective potential above describes the rotational part of the particle’s motion through the angular momentum L and the second term describes the radial part of the potential. The effective potential then incorporates both of these into one “effective” potential – in a sense, it describes the balance between the radial and the angular forces that determine the orbits of a particle.

Anyway, for our purpose, we want to find the minima of this effective potential as an example. The minimum of a radial effective potential generally corresponds to an orbit of constant radius (i.e. a circular orbit ) for the particle. Therefore, the radius r of a circular orbit is found by setting the derivative of the effective potential to zero:

\frac{dV_{eff}\left(r\right)}{dr}=0\ \ \Rightarrow\ \ \frac{d}{dr}\left(\frac{L^2}{2mr^2}+V\left(r\right)\right)=0

Calculating this derivative, we get the following condition for a circular orbit:

\frac{dV\left(r\right)}{dr}=\frac{L^2}{mr^3}

So, given a central potential V(r), we would solve this equation to find the minimum of the effective potential, which describes the possible circular orbits a particle can have under this particular central potential. As an example, we could look at a gravitational potential energy (near a central mass M) of the form:

Plugging this into the equation above and solving for r, we find:

\frac{d}{dr}\left(-\frac{GMm}{r}\right)=\frac{L^2}{mr^3}

\Rightarrow\ \ \frac{GMm}{r^2}=\frac{L^2}{mr^3}

So, we find that a particle with a given constant angular momentum L can have a circular orbit with radius L²/GM around a gravitating central mass M.

This is just one particular example of finding extrema of single-variable functions, but an extremely useful one. Finding minima of effective potential functions is used, for example, to find circular orbits of a charged particle in an electric field or even relativistic circular orbits around a black hole.

Calculus of variations is based on a similar idea. It is the study of finding extremal points of something called functionals, which are essentially functions of other functions. In this sense, variational calculus is just a generalization of finding extremal points of single-variable functions.

The only thing is that the extremal “points” of a functional are not really points, but rather entire functions – functions that either maximize, minimize or make stationary a given functional. So, the entire goal of variational calculus is to find the stationary “points” (extrema) of functionals and these extrema themselves are some kind of functions that depend on the particular problem at hand.

Why Should We Care About Calculus of Variations?

Before we discuss calculus of variations in detail, it’s worth discussing why we would want to do so in the first place. To put it simply, calculus of variations is one of the most important areas of math to master if you want to understand advanced physics, such as quantum field theory or general relativity.

The main reason for this is the fact that almost all our modern theories of physics are described by an action principle. In short, this means that the dynamics of any given theory (such as the dynamics of the electromagnetic field) can be encoded into a quantity called the action – which surprise, surprise, is a functional.

Then, the actual dynamics of the given theory (the “field equations” if we’re talking about a quantum field theory, for example) are found by making the action functional stationary through something called the principle of stationary action – again, requiring the tools of variational calculus. This is generally the way in which all field theories are formulated.

However, calculus of variations comes up even in classical mechanics in a formulation called Lagrangian mechanics. In Lagrangian mechanics, we describe the dynamics of a mechanical system by finding stationary solutions to an action functional – using calculus of variations. These solutions are the solutions to the equations of motion for the system, which are the same solutions we would get by using Newton’s laws.

So, calculus of variations allows us to describe all of classical mechanics using the Lagrangian formulation instead of Newton’s laws. It turns out that the Lagrangian formulation is much more powerful and more general than Newton’s laws, making this an extremely useful application of variational calculus. We’ll discuss Lagrangian mechanics more later.

Calculus of variations also shows up quite frequently in various geometric applications. A typical example of where variational calculus comes up is if we want to find the minimum distance between any two points, say, in the x,y -plane (or on some complicated surface).

In this case, the distance itself would be described by a functional called the arc length functional. To minimize this arc length functional (i.e. find its stationary “points”) then means to find some curves y(x) that minimize (or more generally, make stationary) the arc length functional. We, of course, do this using calculus of variations.

More generally, this problem of finding minimal distances between two points is the problem of finding geodesics in various geometric spaces and it is what a large portion of differential geometry is about. Therefore, variational calculus is extremely important for differential geometry and also for general relativity, since it general relativity based on the mathematics of differential geometry!.

Hopefully all of this work as a bit of motivation for why you should want to learn calculus of variations. We’ll look at lots of examples and physics applications later, which should make it even more clear that calculus of variations is an area of math you really should want to learn.

Functionals

Calculus of variations is all about working with functionals, so let’s talk about these in more detail.

As mentioned earlier, in the simplest sense, a functional is a “function of a function” – that is, a thing that takes in an entire function as its input and returns a number, describing the value of the functional at that “point” (again, not really a point, but rather an entire function).

In contrast, a basic single-variable function would take in just a number, the value of a variable x, for example and return another number that describes the value of the function at that point.

Now, there are certainly more rigorous ways to define functionals, but for our purposes, we’re specifically interested in functionals that take in some function, usually a single-variable function and return a number – so functions of functions. But how do we express such a thing mathematically?

Well, perhaps your first guess might be something of the form:

F\left(y\right)=\left(y\left(x\right)\right)^2

This would indeed be a “function of a function” – it takes in an entire function y(x) as its input. However, this does NOT return a number, instead it returns another function of the variable x. For example, if you were to plug in y(x)=x², you’d get F(x)=x⁴. So, this is not a valid functional.

Generally, a valid functional that takes in a full function and always returns just a single number can be obtained by writing the functional as a definite integral. For example, something of the following form would be a valid functional:

F\left(y\right)=\int_0^1\left(y\left(x\right)\right)^2dx

This would now take in a function y(x) and return just a number instead of a new function of x. We can see this by plugging in, for example y=x², which gives the following value of F:

F=\int_0^1\left(x^2\right)^2dx=\int_0^1x^4dx=\frac{1}{5}\bigg/_{\!\!\!\!\!0}^1x^5=\frac{1}{5}

In general, we write functionals in the form of a definite integral. For a general functional, its integrand (the expression inside the integral) does not have to involve just y(x), it can also also involve x itself, the derivative of y(x), dy(x)/dx, or any number of higher derivatives of y(x).

However, in our case, we’re most often interested in functionals with their integrands being some function that involve just x, y(x) or dy(x)/dx and not other, higher derivatives. These are the most common types of functionals encountered in physics and geometry.

So, the general form of a functional we’re going to be interested in can be written as:

F\left(y\right)=\int_{x_1}^{x_2}f\left(x{,}\ y\left(x\right){,}\ \frac{dy\left(x\right)}{dx}\right)dx

The reason such functionals are interesting to us is because the action functionals used in Lagrangian mechanics and in field theories are of this form – functional with their integrand involving up to first order derivatives only.

In Lagrangian mechanics, the action functionals, S(q), will be integrals with the integrand being a function called the Lagrangian. The Lagrangian is generally a function of time t, the coordinates q_i(t) describing a given system and the time derivatives of the coordinates, dq_i(t)/dt. The action functional then returns a number, the value of the action for any particular set of coordinates, q_i(t), called the trajectory or configuration of the system:

S\left(q\right)=\int_{t_1}^{t_2}L\left(t{,}\ q_i\left(t\right){,}\ \frac{dq_i\left(t\right)}{dt}\right)dt

Again, we will discuss Lagrangian mechanics more in a later lesson.

Other, more explicit functionals we will come to see are, for example, the arc length functional describing the distance between two points, x₁ and x₂, along some curve y(x) in the x,y-plane:

F\left(y\right)=\int_{x_1}^{x_2}\sqrt{1+\left(\frac{dy\left(x\right)}{dx}\right)^2}dx

In this functional, we have the integrand as:

f\left(x{,}\ y{,}\ \frac{dy\left(x\right)}{dx}\right)=\sqrt{1+\left(\frac{dy\left(x\right)}{dx}\right)^2}

F\left(y\right)=\int_{x_1}^{x_2}\sqrt{1+y'^2}dx

The Variation of a Functional

Now, just like we can take the derivative of a single-variable function, we can also take the derivative of a functional. This is called a variation (hence the name ‘variational calculus’).

Just like the derivative of a single-variable function y(x) describes how the value of the function y(x) changes if we change its input variable x by a little bit, the variation of a functional F(y) describes how the value of the functional F(y) changes if we change its input function y(x) by a little bit.

We typically denote variations by the letter δ. So, the variation in a functional F(y) would be denoted as δF(y).

But, how do you actually calculate the variation in a functional? Well, it’s actually not too different from how we would calculate the differential of a typical multivariable function – all of the typical derivative rules like the product rule and the chain rule also apply to calculating variations.

In particular, the differential df(x,y) of a multivariable function f(x,y) describes how the function f changes with respect to all of its inputs (x and y) and is calculated as:

df\left(x{,}y\right)=\frac{\partial f\left(x{,}y\right)}{\partial x}dx+\frac{\partial f\left(x{,}y\right)}{\partial y}dy

Here, we essentially just have the sum of the “changes in f with respect to all its variables multiplied by the changes in the variables themselves” (we covered this in the lesson on multivariable calculus):

The same idea applies to the variation of a functional. The variation of a functional F(y) describes how the value of the integrand f(x,y,y’) of the functional (and thus, the value of the functional itself) changes with respect to a small change in the function y(x).

Therefore, the variation in the integrand f(x,y,y’) consists of both a contribution from changing y, but also from changing y’ (we will typically treat these two as independent functions). The “formula” for the variation in a functional F is then given by:

\delta F=\int_{x_1}^{x_2}\left(\frac{\partial f}{\partial y}\delta y+\frac{\partial f}{\partial y'}\delta y'\right)dx

Here we have the exact same kind of “sum of changes in f with respect to the variables we’re interested in multiplied by the changes in the variables themselves”.

You may wonder whether this formula above should also have a contribution coming from varying the variable x itself, resulting in a term like (∂f/∂x)δx. The answer is no – when looking at the variation of this functional, we’re specifically interested in how the functional changes with respect to the actual function in its argument, y(x), but we’re NOT changing the independent variable x itself.

Now, there is a lot to take in here, but the reason we covered all of this is because calculating the variation of a functional allows us to find extrema of a functional in a similar way as in the case with a single-variable function.

In particular, we find the extremal “points” (the functions y(x) that make the functional F stationary) of a functional F by setting its variation to zero:

This is quite similar to the case of a single-variable function when setting df(x)/dx=0, but instead of getting an algebraic equation we would solve for the value of x, we actually get a differential equation we will have to solve to find the functions y(x) that make the original functional stationary.

This will be the topic of the next lesson, which should make everything more clear.

Vector Calculus For Physics: A Complete Self-Study Course

Functionals & Variations

Brief Introduction To Calculus of Variations

Why Should We Care About Calculus of Variations?

Functionals

The Variation of a Functional

Modal title