Gradient, Divergence, Curl & Laplacian

Vector calculus, to put it simply, is the study of combining calculus concepts with vectors. The point of vector calculus is really to answer the following question; how do we differentiate (and integrate) vectors in a useful and sensible way?

We now have all the tools we need to answer such a question. In this lesson, we’ll apply both multivariable calculus and vector operations to develop a calculus of vectors.

Lesson Contents

Differential Operators On Scalar & Vector Fields

To differentiate a vector, we need a vector field. This is simply because it’s not useful at all to differentiate an “ordinary” vector that has some constant numbers as components. We need a vector that has components that are functions of our coordinates, which is a vector field.

We can also differentiate a scalar field. Scalar fields are generally just multivariable functions, so we can certainly take derivatives of them.

In this lesson, we’ll go over various differential operators that act on either scalar or vector fields. An operator, in this context, is simply a thing that takes either a vector field or scalar field and outputs a different vector or scalar field.

In all of these cases, we’ll discuss these operators mainly using Cartesian coordinates (x,y,z).

You’ll find a table of all the different operators and their formulas at the end of this article (in the “Lesson Summary” -section).

Gradient

The first operator we’ll discuss is the gradient.

The gradient acts on a scalar field and produces a vector field as a result (we’ll to be precise, the gradient produces something called a covector, but we’ll come to this later; using Cartesian coordinates, however, this makes no difference).

The gradient is typically denoted by the nabla-symbol (∇) with a vector sign above it to denote the fact that it outputs a vector (in Cartesian coordinates).

The operation of the gradient on a scalar field is defined as follows (in Cartesian coordinates):

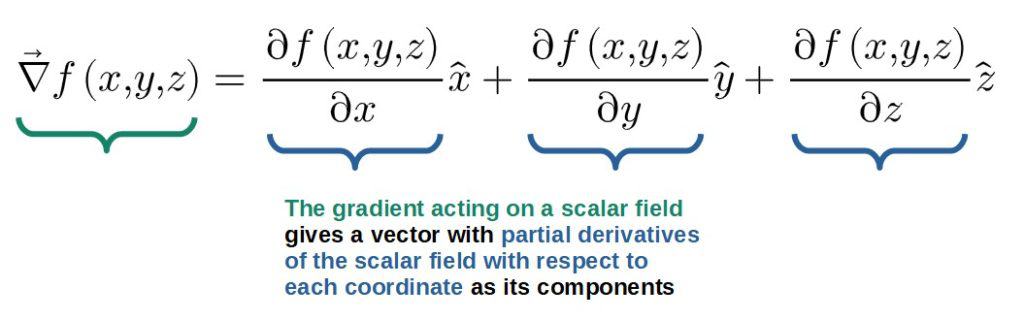
Geometrically, this gradient vector describes the direction of “fastest rate of change” of the scalar field.

So, if you were to imagine a hill with the height described by the value of a scalar function (in 2D), the gradient vector would be pointing in the steepest direction along the hill.

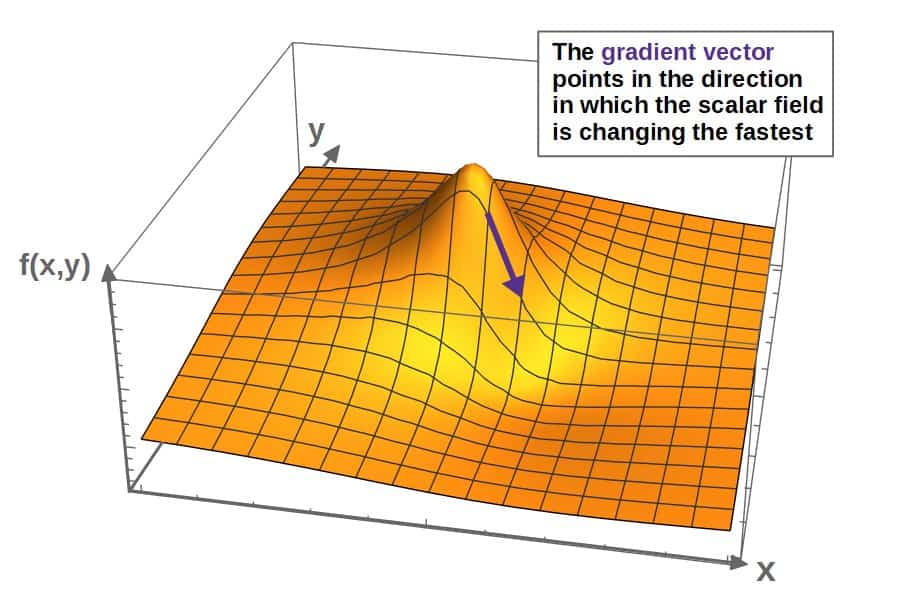
The numerical amount of the rate of change is the magnitude of the gradient vector.

Physics Example: Electric Field as The Gradient of Electric Potential

In electrostatics (when the electric and magnetic fields are not varying with time), an electric field can always be written as the (negative) gradient of a scalar field called the electric potential:

We’ll see in later lessons where this actually comes from (it comes from something known as the Helmholtz decomposition theorem), but essentially the electric potential gives us an alternative way to calculate electric fields.

In fact, it’s often easier to first find the electric potential of some charge configuration and then calculate the electric field by taking the gradient, instead of actually directly trying to find the electric field.

Anyway, let’s do a simple example to illustrate how the gradient can be used. Consider an electric potential of the following form:

Vleft(x{,}yright)=frac{q}{4pivarepsilon_0sqrt{x^2+y^2}}

This happens to be the electric potential generated by a point charge q (at the origin). We can visualize this potential as essentially a “hill” with the point charge q sitting on top of the hill (which would be infinitely far up):

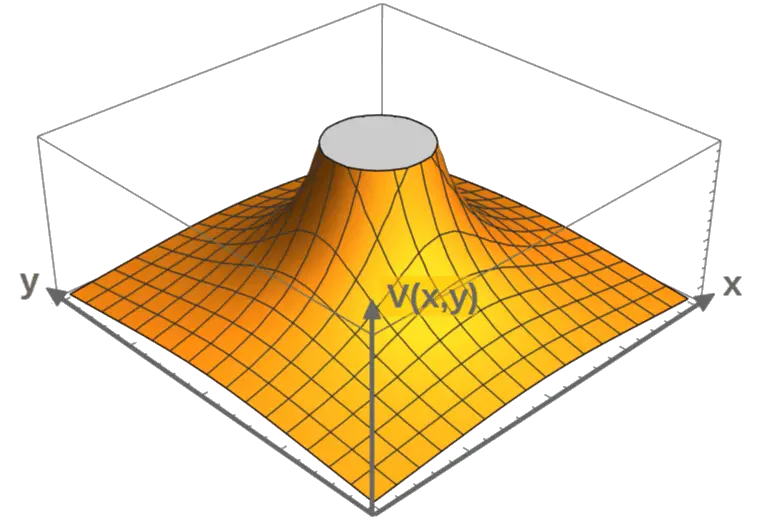
Anyway, to find the electric field, let’s first calculate the partial derivatives of this potential (note that this is only in 2D):

frac{partial V}{partial x}=frac{q}{4pivarepsilon_0}frac{partial}{partial x}frac{1}{sqrt{x^2+y^2}}=-frac{q}{4pivarepsilon_0}frac{x}{left(x^2+y^2right)^{frac{3}{2}}}

frac{partial V}{partial y}=frac{q}{4pivarepsilon_0}frac{partial}{partial y}frac{1}{sqrt{x^2+y^2}}=-frac{q}{4pivarepsilon_0}frac{y}{left(x^2+y^2right)^{frac{3}{2}}}

The gradient (electric field) is then:

vec{E}=-vec{∇}V=-frac{partial V}{partial x}hat{x}-frac{partial V}{partial y}hat{y}

vec{E}=frac{q}{4pivarepsilon_0}frac{x}{left(x^2+y^2right)^{frac{3}{2}}}hat{x}+frac{q}{4pivarepsilon_0}frac{y}{left(x^2+y^2right)^{frac{3}{2}}}hat{y}

The electric field of this point charge is then (in Cartesian coordinates):

vec{E}left(x{,}yright)=frac{q}{4pivarepsilon_0}frac{1}{left(x^2+y^2right)^{frac{3}{2}}}left(xhat{x}+yhat{y}right)

We can visualize this electric field as a vector field in the Cartesian xy-plane (with the charge q that generates this field sitting at the middle as the “source” of the electric field):

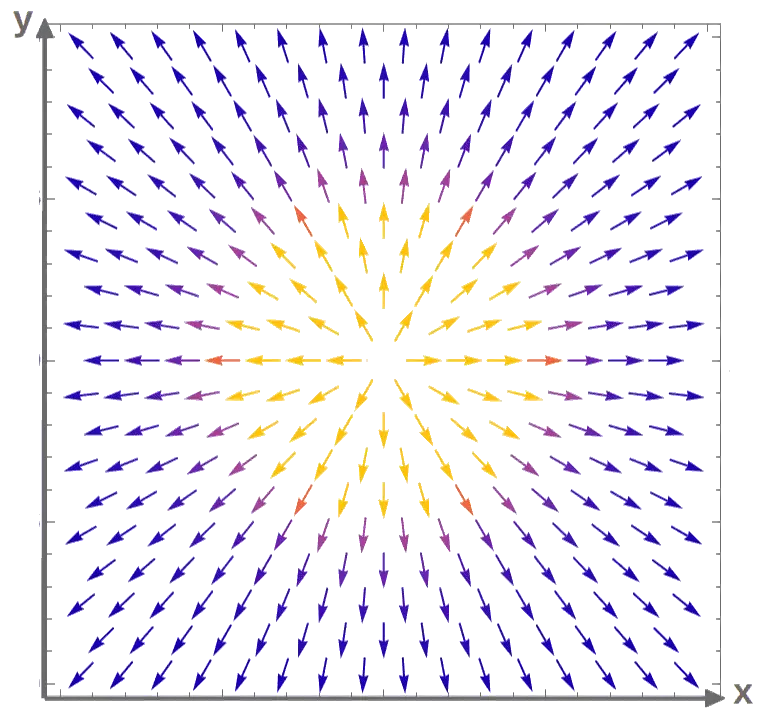
Essentially, these field arrows represent the force another charge would experience if it was placed in this field; a positive charge would get “repulsed” away from the center, while a negative charge would get “attracted” towards the center.

Now, this electric field is typically written in polar coordinates, so we can convert this by first writing the electric field in the following form (you’ll see why soon):

vec{E}left(x{,}yright)=frac{q}{4pivarepsilon_0}frac{1}{x^2+y^2}left(frac{x}{sqrt{x^2+y^2}}hat{x}+frac{y}{sqrt{x^2+y^2}}hat{y}right)

We can now use the Cartesian-to-polar relations:

x=rcostheta Rightarrow costheta=frac{x}{r}

y=rsintheta Rightarrow sintheta=frac{y}{r}

We know that r (the “radial distance”) is given r=√(x²+y²), so we have:

frac{x}{sqrt{x^2+y^2}}=costheta {,} frac{y}{sqrt{x^2+y^2}}=sintheta

These are exactly what we have inside the parentheses in the electric field expression! Inserting these and r²=x²+y², we then have:

Rightarrow vec{E}left(rright)=frac{q}{4pivarepsilon_0}frac{1}{r^2}left(costhetahat{x}+sinthetahat{y}right)

This thing inside these parentheses is nothing but the radial unit basis vector in polar coordinates (go back to the first lesson if you don’t remember the formula for that).

All in all, we get the electric field in polar coordinates (which is only a function of the radial distance r):

vec{E}left(rright)=frac{q}{4pivarepsilon_0}frac{hat{r}}{r^2}

Now, there are certainly much easier ways to obtain the same result by using the gradient directly in polar coordinates. However, this illustrates the use of the gradient in Cartesian coordinates quite well, which is what we’re interested in for now.

Directional Derivative

Now, you may ask whether it would be possible to describe the rate of change of a scalar field in any direction, not just in the direction of fastest rate of change (which is what the gradient describes).

This is indeed possible using an operator known as the directional derivative. We can describe any direction in space by specifying a vector in that particular direction (it helps to think of the vector as “an arrow in space”).

The directional derivative describes the rate of change of a scalar field in the direction of some particular vector. I’m going to denote the directional derivative as:

This describes the rate of change of the scalar field of in the direction of the vector v.

Now, the directional derivative can be computed as follows:

vec{nabla}_{vec{v}}f=vec vcdotvec nabla f

In other words, we’re calculating the gradient of f, which describes the “rate of change of f” and then taking the particular component of this resulting vector that is in the direction of v. The result is the rate of change of f in the direction of v.

Writing out the dot product (in Cartesian coordinates), we get a formula for the directional derivative:

vec{nabla}_{vec{v}}f=v_xfrac{partial f}{partial x}+v_yfrac{partial f}{partial y}+v_zfrac{partial f}{partial z}

As a sidenote, the directional derivative is actually really important if you want to understand differential geometry. This is because the concept of a directional derivative can be extended to vector fields and tensor fields as covariant derivatives and Lie derivatives, which are absolutely central concepts in differential geometry as well as in many areas of physics that utilize concepts from differential geometry (such as general relativity).

Divergence

So far, we’ve only talked about operations on scalar fields.

First of all, the gradient by itself only acts on scalar fields, not vector fields (although in more advanced tensor analysis, we can define a vector gradient as well).

For a vector field, a similar operator to the gradient can be calculated, but using a dot product instead.

This operator is called the divergence and it acts on a vector field to produce a scalar field (similarly to how the dot product between two vectors gives a scalar):

The result on the right-hand side here is just a scalar as it is doesn’t contain any separate vector components. Also, note that here I’m writing the components of f (f_x,f_y,f_z) with downstairs indices, but we’ll soon come to the fact that the generally correct way to write these would be with upstairs indices (though in Cartesian coordinates, this makes no difference).

Geometrically, the divergence of a vector field represents how much the vector field arrows are “spreading out” at any given point.

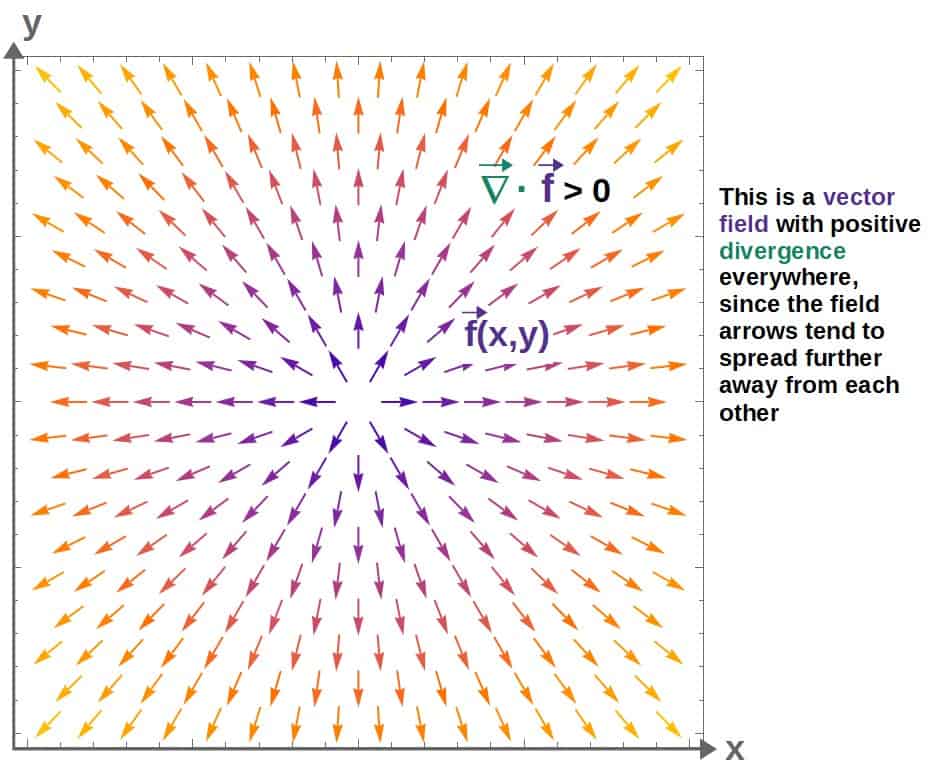
A vector field with negative divergence would be a vector field that would point “inwards”, towards the origin everywhere, instead of away from the origin, like we have here.

One way to perhaps better picture this is by imagining this vector field describes the flow of a fluid of some sorts. The divergence would then measure the amount of the fluid “flowing in” compared to “flowing out” at any given point.

So, for a positive divergence, there would be more fluid flowing out of a point than into the point, so you could imagine that there is some kind of “source” of the fluid there.

In general, the divergence of a vector field at any given point can be thought of as a source of the vector field.

This analogy works very well in electromagnetism, where the “sources” of an electric field are electric charges, which create either a positive or a negative divergence of the electric field.

Physics Example: Divergence of Electric and Magnetic Fields

Electric fields are essentially vector fields that describe the direction and magnitude of the electric force that a charged particle would experience if it was placed in the field.

Electric fields are always generated by electric charges. In fact, electric charges act as sources of an electric field by creating an electric field with non-zero divergence.

In particular, a positive electric charge creates an “outward pointing” electric field (i.e. positive divergence), while a negative electric charge creates an “inward pointing” electric field (negative divergence).

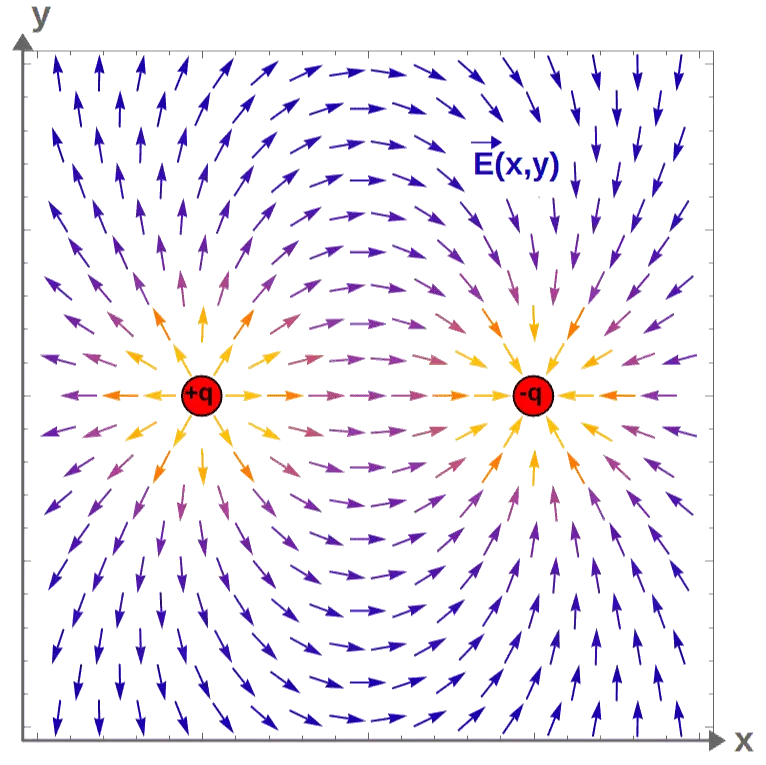
This is the electric field of an electric dipole, i.e. a system of two stationary charges, +q and -q.

Mathematically, this is described by Gauss’s law (one of Maxwell’s equations), which states that the divergence of the electric field is proportional to the charge density:

vec{∇}cdotvec{E}=frac{rho}{varepsilon_0} — This ε₀ is a constant known as the vacuum permittivity.

From this, we can see that if there is a positive charge density at a point, the divergence will be positive, which acts as a source of the electric field. Similarly, a negative charge density would act as a “sink” in the electric field.

This can also be used to calculate various things. Let’s say we have an electric field of the form:

vec{E}left(x{,}yright)=frac{rho_0x}{3varepsilon_0R}sqrt{x^2+y^2}hat{x}+frac{rho_0y}{3varepsilon_0R}sqrt{x^2+y^2}hat{y} — Here, ρ₀ and R are constants with units of C/m³ and m.

This actually happens to describe the electric field inside a non-uniformly charged sphere. Anyway, let’s find the charge distribution (charge density function ρ(x,y)) that generates this particular electric field by using Gauss’s law:

vec{∇}cdotvec{E}left(x{,}yright)=frac{rholeft(x{,}yright)}{varepsilon_0}

Let’s begin by calculating the partial derivatives of the electric field components (we need these for the divergence):

frac{partial E_x}{partial x}=frac{rho_0}{3varepsilon_0R}frac{partial}{partial x}left(xsqrt{x^2+y^2}right)=frac{rho_0}{3varepsilon_0R}left(sqrt{x^2+y^2}+frac{x^2}{sqrt{x^2+y^2}}right)

frac{partial E_y}{partial y}=frac{rho_0}{3varepsilon_0R}frac{partial}{partial y}left(ysqrt{x^2+y^2}right)=frac{rho_0}{3varepsilon_0R}left(sqrt{x^2+y^2}+frac{y^2}{sqrt{x^2+y^2}}right)

The divergence is then:

vec{∇}cdotvec{E}=frac{partial E_x}{partial x}+frac{partial E_y}{partial y}=frac{rho_0}{3varepsilon_0R}left(sqrt{x^2+y^2}+frac{x^2}{sqrt{x^2+y^2}}right)+frac{rho_0}{3varepsilon_0R}left(sqrt{x^2+y^2}+frac{y^2}{sqrt{x^2+y^2}}right)

This can be simplified further:

vec{∇}cdotvec{E}=frac{rho_0}{3varepsilon_0R}left(2sqrt{x^2+y^2}+frac{x^2+y^2}{sqrt{x^2+y^2}}right)=frac{rho_0}{varepsilon_0R}sqrt{x^2+y^2} — Here I’ve used the fact that (x²+y²)/√(x²+y²)=√(x²+y²).

The charge density can then be obtained from Gauss’s law:

rholeft(x{,}yright)=varepsilon_0vec{∇}cdotvec{E}=frac{rho_0}{R}sqrt{x^2+y^2}

Now, this is just one example of how the concept of divergence can be used in physics and electromagnetism.

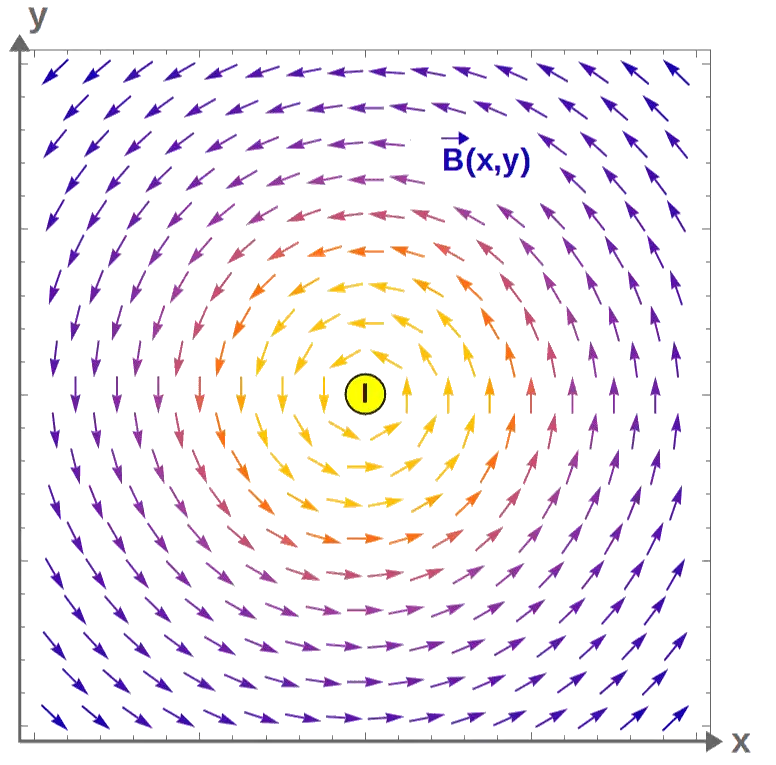
Anyway, on the other hand, Gauss’s law for a magnetic field states that the divergence of the magnetic field is always zero:

This essentially means that there is no magnetic field “sources”, i.e. magnetic charges. This is nothing but the statement that magnetic monopoles do not exist.

Therefore, vector fields describing a magnetic field can only “circulate” around a point (this property is known as curl), but cannot spread away from it.

Magnetic fields are fundamentally generated by moving charges (i.e. currents). Here we have a current I *flowing towards* the screen, which generates a magnetic field that circulates around it.

Curl

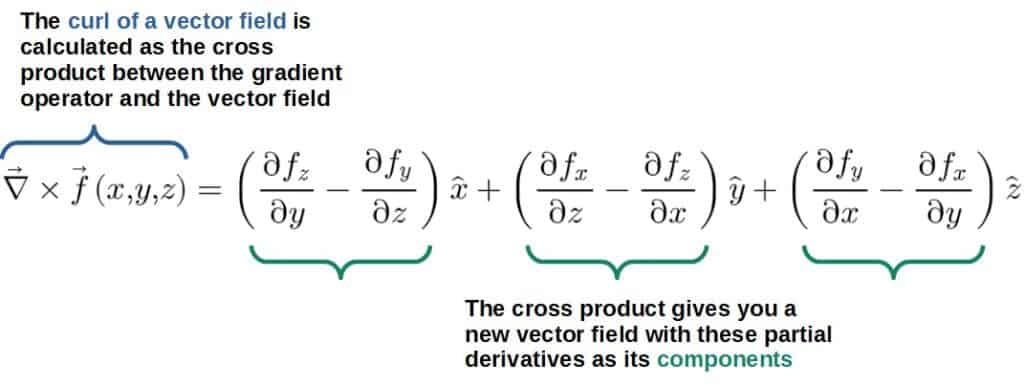
Another way we could define a differential operator that acts on a vector field would be an operator that produces another vector field as a result. This is called the curl and it is defined using the cross product:

Geometrically, the curl of a vector field represents how the vector field tends to circulate around any given point.

This can be best visualized in two dimensions (however, note that the cross product would technically be defined in 3D only):

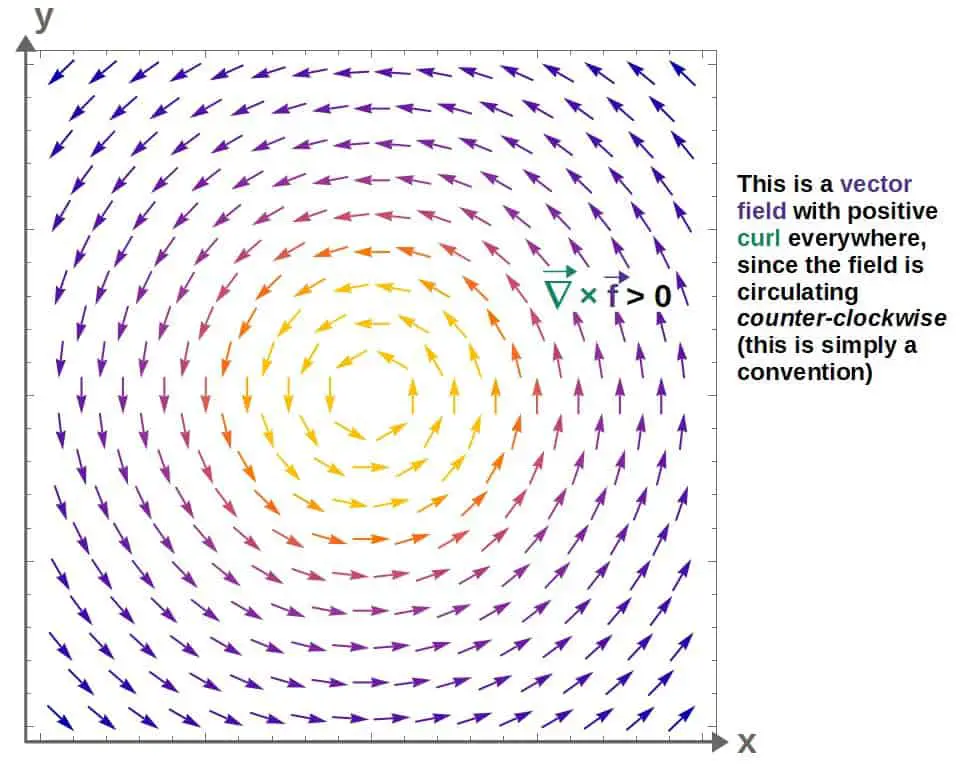
The actual direction of the curl vector at each point would be pointing out of the screen towards you.

This is determined by the right-hand rule by essentially curling the four fingers (starting from the index finger) on your right hand along the “circulation” of this vector field; your thumb would then point in the direction of the actual cross product vector. This is, however, just a convention.

Now, since the curl is really a differential operator, it’s worth keeping in mind that the curl describes the “circulation” of a vector field at a single point.

You can then kind of imagine the curl of a vector field as a kind of “circulation density”, similarly to how the divergence could be thought of as the “flow density” or a source/sink of the vector field.

Physics Example: Curl of Electrostatic and Magnetostatic Fields

In electrostatics (i.e. in situations where the electric and magnetic fields are not varying with time), the curl of the electric field is always zero, according to Faraday’s law (one of Maxwell’s equations):

Essentially, this just means that the electric field only tends to “diverge” away from a point, but not “circulate” around it.

Now, more interestingly, the curl of the magnetic field at any point is proportional to the current density at that point, given by Ampère’s law:

vec{∇}timesvec{B}=mu_0vec{J} — This constant μ₀ is called the vacuum permeability,

This essentially tells us that the curl of a magnetic field is generated by currents. Similarly to Gauss’s law for the electric field, this can also be used to calculate stuff.

Let’s, for example, take a magnetic field of the form:

vec{B}left(x{,}yright)=-frac{mu_0Iy}{2pi R^2}hat{x}+frac{mu_0Ix}{2pi R^2}hat{y}+0hat{z} — The I and R here are constants, representing current and radius of the cross-sectional area that the current is flowing through.

This actually represents the magnetic field inside a cylindrical wire with uniform current density. But, let’s see what we get if we were to calculate the curl of this.

In general, the curl is given by the formula:

vec{∇}timesvec{B}=left(frac{partial B_z}{partial y}-frac{partial B_y}{partial z}right)hat{x}+left(frac{partial B_x}{partial z}-frac{partial B_z}{partial x}right)hat{y}+left(frac{partial B_y}{partial x}-frac{partial B_x}{partial y}right)hat{z}

Since the B-field in our case does not depend on z and its z-component is zero, all of the partial derivatives involving z are automatically zero. Thus, the curl has just one component and it becomes:

vec{∇}timesvec{B}=left(frac{partial B_y}{partial x}-frac{partial B_x}{partial y}right)hat{z}

These partial derivatives are given by:

frac{partial B_y}{partial x}=frac{mu_0I}{2pi R^2}frac{partial}{partial x}x=frac{mu_0I}{2pi R^2}

frac{partial B_x}{partial y}=-frac{mu_0I}{2pi R^2}frac{partial}{partial y}y=-frac{mu_0I}{2pi R^2}

Thus, we have the curl of the magnetic field:

vec{∇}timesvec{B}=left(frac{mu_0I}{2pi R^2}-left(-frac{mu_0I}{2pi R^2}right)right)hat{z}=frac{mu_0I}{pi R^2}hat{z}

Now, by Ampère’s law, the current density is given by:

vec{J}=frac{1}{mu_0}vec{∇}timesvec{B}=frac{I}{pi R^2}hat{z}

So, we get a constant current density with magnitude I/πR², which is just the current per unit cross-sectional area of the cylindrical wire (any cross-section of a cylinder is a circle with area A=πR²), flowing in the z-direction (perpendicularly to the xy-plane where the magnetic field is circulating around).

Laplacian

The last one of these differential operators we’re going to discuss has to do with second derivatives. In particular, second derivatives of scalar fields.

The Laplacian operator (denoted as either ∇² or Δ) itself is defined as the dot product between two “gradient vectors”:

nabla^2=Delta=vec{nabla}cdotvec{nabla}=frac{partial^2}{partial x^2}+frac{partial^2}{partial y^2}+frac{partial^2}{partial y^2} — This expression on the right-hand side may seem weird and that’s because it is. The Laplacian is an operator, so it has to act on something and it doesn’t really make sense to write it by itself like this.

The Laplacian acts on a scalar field to output another scalar field:

nabla^2fleft(x{,}y{,}zright)=frac{partial^2fleft(x{,}y{,}zright)}{partial x^2}+frac{partial^2fleft(x{,}y{,}zright)}{partial y^2}+frac{partial^2fleft(x{,}y{,}zright)}{partial y^2} — Note; it is also possible to construct a Laplacian that acts on a vector field to give another vector field.

Geometrically, the value of the Laplacian of a scalar field at some particular point represents the average difference between the values of the scalar field at that point and its surrounding points.

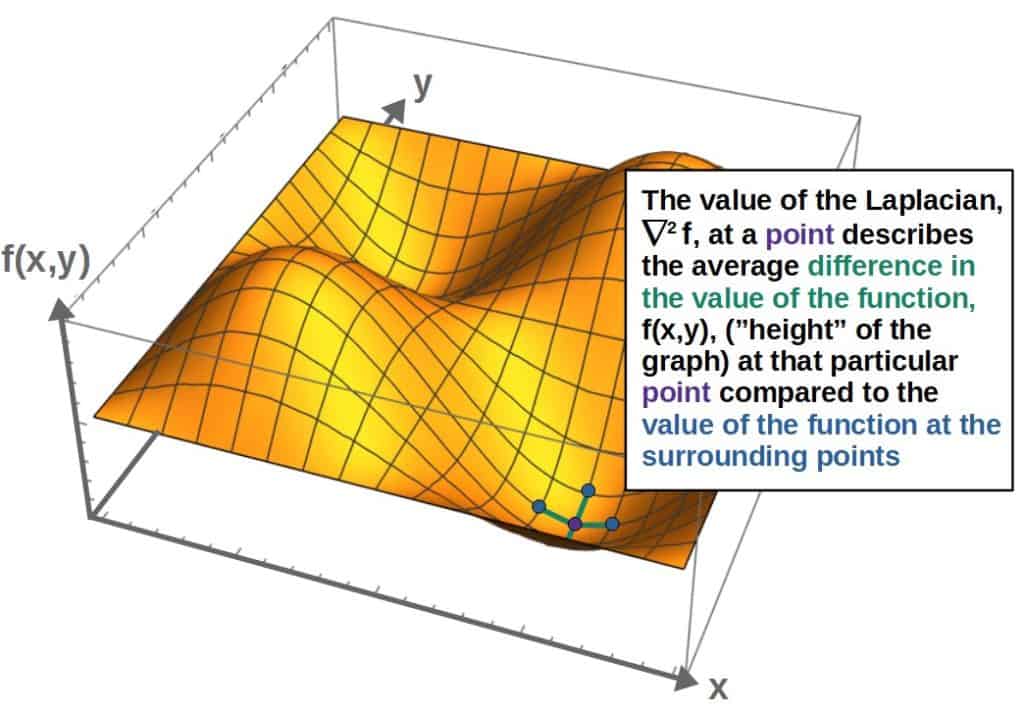
So, if the Laplacian of a scalar field happens to be positive at some point, it means that the value (“height”) of the field is larger, on average, at the surrounding points.

In other words, the value of the Laplacian would be positive at minimum points on the graph of a scalar field (these “pits” you see in the picture above) since at these minima, all the surrounding points have a larger value.

On the other hand, the Laplacian being negative at some point would mean that, on average, the points surrounding that particular point of interest have a smaller value of the scalar field.

This would occur, for example, at the maximum points of the scalar function (on top of the “hills” you see above) since at these points, the value of the field is smaller at all the surrounding points.

At points where the function is flat, the value of the Laplacian would be approximately zero, since all the surrounding points are at the same value and thus, the average difference of the function’s values at these points is zero.

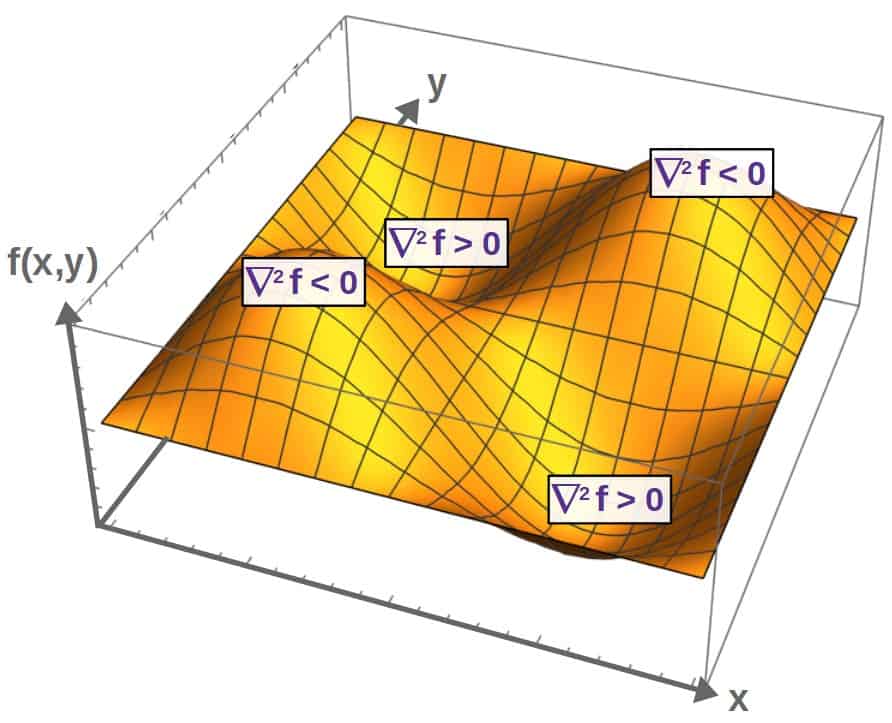
Now, the key here is the word ‘average difference’.

In other words, the Laplacian of a scalar field can be thought of as taking a point as its input, comparing the value of the scalar field at that point to all of the “surrounding points” (that are infinitesimally close) and then taking the average difference of these values compared to the value of the scalar field at the particular point of interest.

The Laplacian also, in a sense, tells you about the “shape” or average curvature of the scalar field at a point; if the Laplacian has a large value, the surrounding points, on average, have a much larger value and the function will be highly “curved”.

Now, in my opinion, the most intuitive physical explanation of the Laplacian comes from the heat equation. You’ll find an explanation (as well as a little animation I made) below.

Physics Example: Heat Equation and The Laplacian

The heat equation is a partial differential equation that’s often used to model how the temperature in some region changes with time and throughout space.

Here, we’ll take the temperature to be a function of two spacial coordinates (x and y) as well as time (t). In other words, the temperature varies throughout space, but also changes with time:

The heat equation tells us exactly how this temperature will change over time throughout space:

On the left-hand side, we have the rate of change of the temperature (time derivative) and on the right, we have the Laplacian of the temperature describing, roughly speaking, the average differences in the temperature throughout space.

Now, this equation tells us that the larger the value of the Laplacian at a point, the faster the temperature will change at that point.

In other words, if the difference in temperature at some point, on average, is very large, the temperature t that point will tend to change really quickly with time.

For example, if the Laplacian is positive, this means that the temperature at that point is less that at the surrounding points (again, on average).

Then, according to the heat equation, since the Laplacian is positive, the time derivative will also be positive and the temperature at that point will increase over time.

So, this basically tells us that the heat profile in any given region will change with time in such a way that the average temperature difference throughout space will be zero (i.e. the Laplacian is zero, meaning that the heat does not change with time anymore).

In other words, heat tends to “spread out” over time and reach an equilibrium state when the average temperature is the same everywhere.

Okay, let’s look at a little example. Say we have an initial temperature profile (the temperature in a region at t=0) that looks as follows:

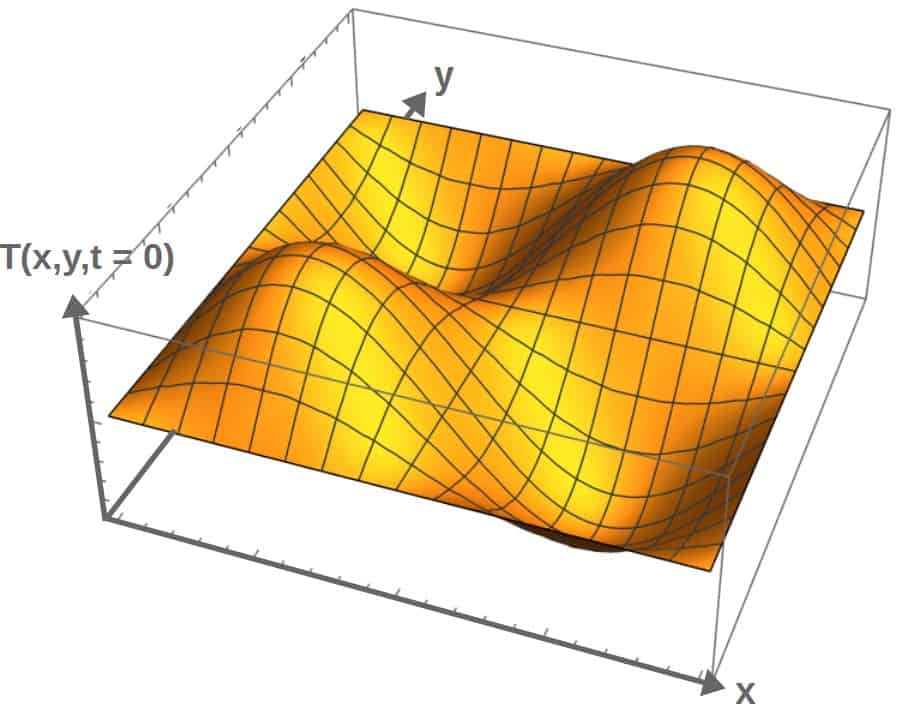
The temperature at any particular point in time can be visualized as a scalar field T(x,y) with the “height” of the graph describing the temperature at that (x,y)-point in space.

As time passes, what would we expect to happen to this temperature profile?

Well, according to the heat equation, the “pits” (the really cold regions) in the graph have a positive Laplacian, so the temperature will increase with time at those points.

On the other hand, the temperature at the “hills” (the hot regions) will decrease with time, since the Laplacian is negative at these points.

So, essentially, the hot regions will become colder and the cold regions hotter with time until eventually, the heat “spreads out” and reaches an equilibrium such that the average difference in temperature is zero everywhere.

Here’s a little animation of exactly what happens when we let this temperature profile evolve in time (according to the heat equation):

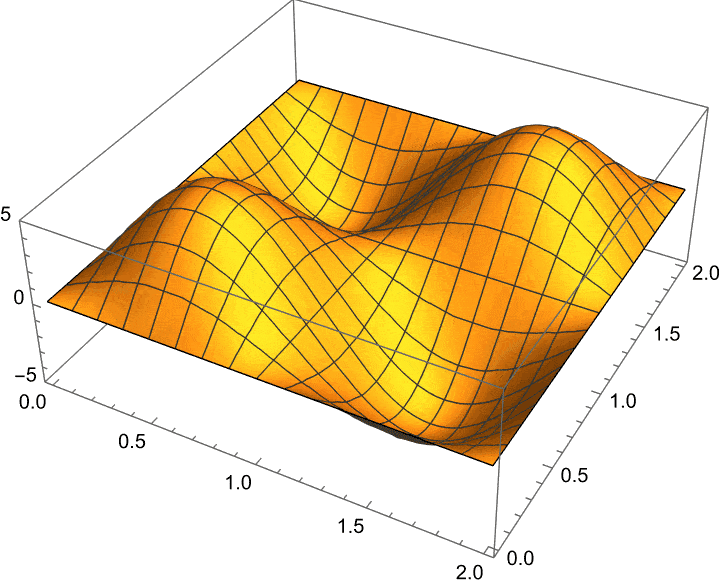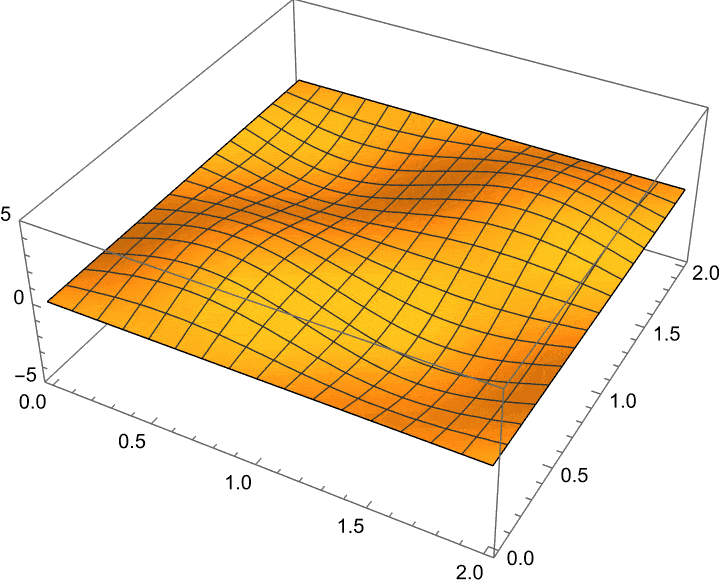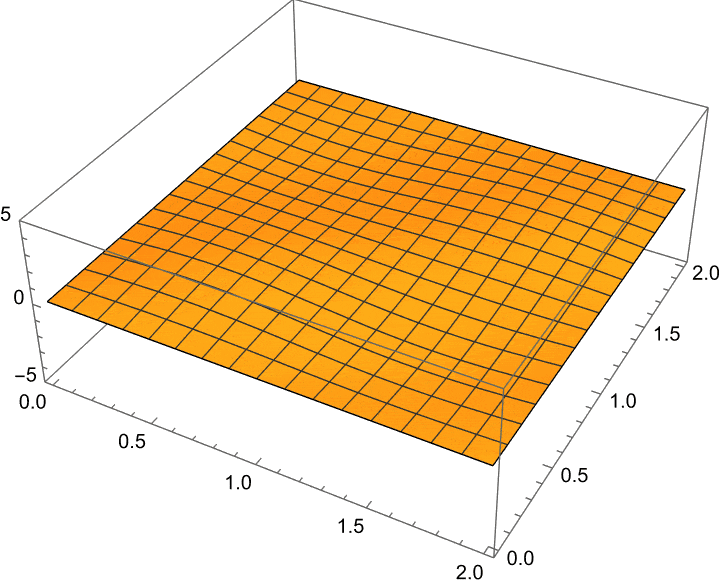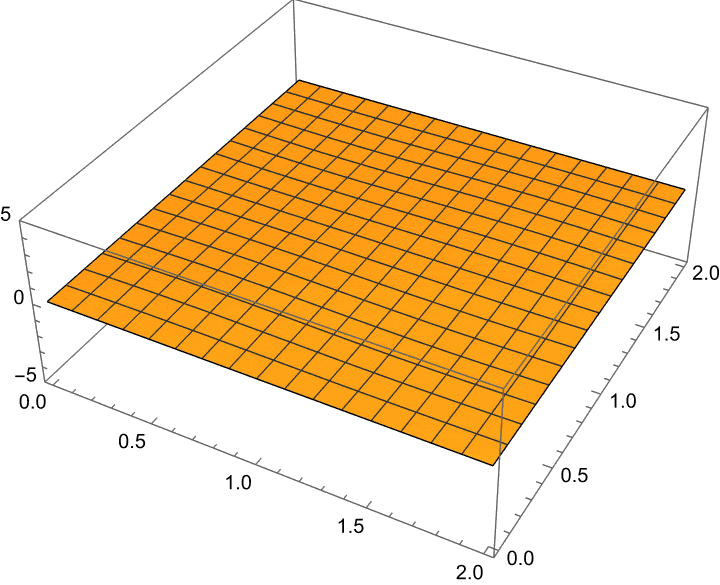
For reference, the actual temperature function here is:

Tleft(x{,}y{,}tright)=T_0sinleft(frac{pi x}{L}right)sinleft(frac{pi y}{L}right)e^{-lambda^2t} — These T₀, L and λ are simply constants with appropriate physical units.

This is indeed a solution to the heat equation, which we can check by just plugging it into the heat equation. The time derivative of this temperature function is:

frac{partial T}{partial t}=-lambda^2T_0sinleft(frac{pi x}{L}right)sinleft(frac{pi y}{L}right)e^{-lambda^2t}

The spacial second derivatives are (simply by differentiating the sin(x) and sin(y) parts twice):

frac{partial^2T}{partial x^2}=-frac{pi^2}{L^2}T_0sinleft(frac{pi x}{L}right)sinleft(frac{pi y}{L}right)e^{-lambda^2t}

frac{partial^2T}{partial y^2}=-frac{pi^2}{L^2}T_0sinleft(frac{pi x}{L}right)sinleft(frac{pi y}{L}right)e^{-lambda^2t}

The Laplacian is then:

∇^2T=frac{partial^2T}{partial x^2}+frac{partial^2T}{partial y^2}=-frac{2pi^2}{L^2}T_0sinleft(frac{pi x}{L}right)sinleft(frac{pi y}{L}right)e^{-lambda^2t}

If this solves the heat equation, we must have:

frac{partial T}{partial t}=∇^2T Rightarrow -lambda^2T_0sinleft(frac{pi x}{L}right)sinleft(frac{pi y}{L}right)e^{-lambda^2t}=-frac{2pi^2}{L^2}T_0sinleft(frac{pi x}{L}right)sinleft(frac{pi y}{L}right)e^{-lambda^2t}

This is indeed true if the following “constraint” is true:

Lesson Summary

The key takeaways from this lesson are:

In vector calculus, the central concepts revolve around differentiating scalar and vector fields.
This is done using various differential vector operators that act on a scalar/vector field to produce another scalar/vector field.
The most common of these operators are the gradient, divergence, curl and Laplacian, which all have their own geometric interpretations.
These operators are some of the most central mathematical tools in many areas of physics, including (but certainly not limited to) electromagnetism and thermodynamics.

Below is also a list of the different operators discussed in this lesson with their formulas and properties included.

vec{∇}f=frac{partial f}{partial x}hat{x}+frac{partial f}{partial y}hat{y}+frac{partial f}{partial z}hat{z}

vec{v}cdotvec{∇}f=v_xfrac{partial f}{partial x}+v_yfrac{partial f}{partial y}+v_zfrac{partial f}{partial z}

Differential operator	Acts on	Formula (in Cartesian coordinates)	Geometric interpretation
Gradient	A scalar field to produce a vector field	$vec{∇}f=frac{partial f}{partial x}hat{x}+frac{partial f}{partial y}hat{y}+frac{partial f}{partial z}hat{z}$	Rate of change in f in the direction of fastest change
Directional derivative	A scalar field to produce another scalar field	$vec{v}cdotvec{∇}f=v_xfrac{partial f}{partial x}+v_yfrac{partial f}{partial y}+v_zfrac{partial f}{partial z}$	Rate of change in f in the direction of the vector v
Divergence	A vector field to produce a scalar field	$vec{∇}cdotvec{f}=frac{partial f_x}{partial x}+frac{partial f_y}{partial y}+frac{partial f_z}{partial z}$	Tendency of the vector field f to spread out from a point
Curl	A vector field to product another vector field	$vec{∇}timesvec{f}=left(frac{partial f_z}{partial y}-frac{partial f_y}{partial z}right)hat{x}+left(frac{partial f_x}{partial z}-frac{partial f_z}{partial x}right)hat{y}+left(frac{partial f_y}{partial x}-frac{partial f_x}{partial y}right)hat{z}$	Tendency of the vector field f to circulate around a point
Laplacian	A scalar field to product another scalar field	$∇^2f=frac{partial^2f}{partial x^2}+frac{partial^2f}{partial y^2}+frac{partial^2f}{partial z^2}$	Average difference between the value of f at a point and the values of f at the surrounding points

Vector Calculus For Physics: A Complete Self-Study Course