Scalar & Vector Fields

The central objects in multivariable calculus and vector calculus are things that vary throughout a given coordinate system or in other words, are functions of coordinates.

For our purposes, these are going to be scalar fields and vector fields.

First of all, we need to understand the concept of a field. A field is simply a function that “takes in” a particular point in space (described by a set of coordinates) and associates some quantity with that point in space.

Now, when I’m talking about “space” I do not necessarily mean “physical space”. I’m generally talking about a mathematical, abstract space (which could be a 3-dimensional physical space as well).

For our purposes, there are two types of fields; scalar fields and vector fields (in general, we may also have tensor fields).

A scalar field associates a scalar to each point in space, while a vector field associates a vector to each point in space.

An example of a scalar field would be the function:

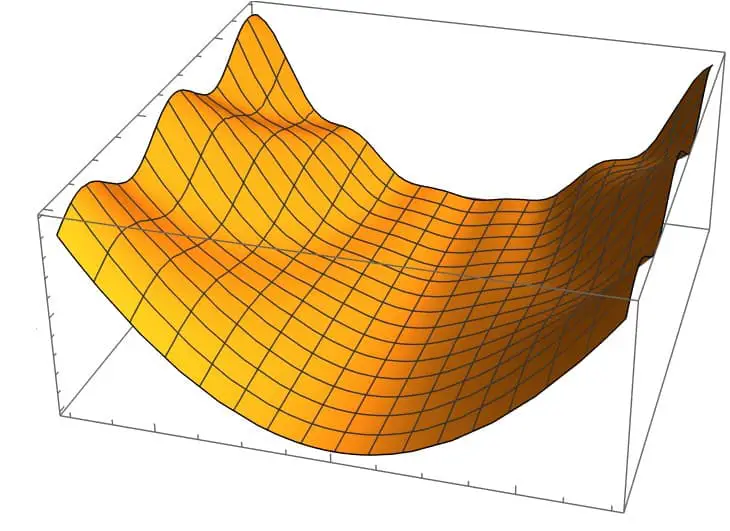
An example of a vector field, on the other hand, would be the function:

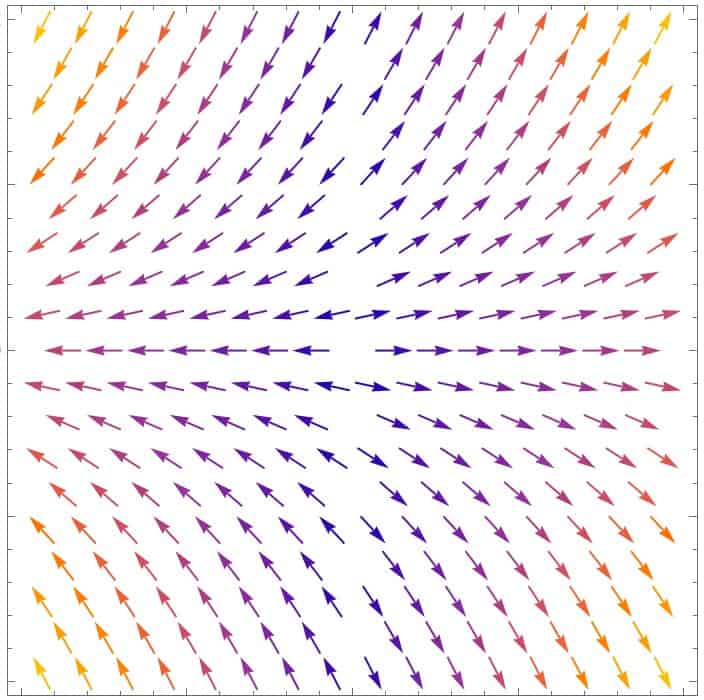
For all practical purposes, a vector field is simply a vector with components that are functions of the coordinates. This means that a vector field “outputs” a different vector for a different set of coordinates.

In contrast, an “ordinary” vector would be, for example:

This is simply a single vector with constant components (4,7,1).

Even though this is a fairly simple concept, it’s important that you understand this distinction between a vector and a vector field, because it turns out that we can extend this exact logic further to tensors and tensor fields as well.

Also, in later lessons we will see how to describe these fields in different coordinate systems by using coordinate transformations.

Why Do We Need Scalar & Vector Fields?

Scalar and vector fields (and tensor fields in general) are perhaps one of the most important objects all throughout physics.

A simple example of a scalar field in physics would be temperature, which may vary from point to point in space. In other words, this would be a scalar field that takes in some point in space (coordinates) and gives you the temperature at that point.

Another, perhaps more interesting example is that of a scalar quantum field in quantum field theory.

For example, the Higgs boson and the Higgs phenomenon are described by a scalar field that is quantized, according to some procedures used in quantum field theory.

In physics, we often want to also include information about directions to our theories, which is where vector fields are extremely useful.

An example of a vector field is the electric field, which takes in a point and outputs a vector.

The magnitude of this vector describes the strength of the electric field at each point (which is proportional to the electric force a particle would feel at that point) and its direction describes the direction of the electric force a charged particle would experience at each point.

Also, vector fields in quantum field theory lead to polarized quantum fields (which kind of contain information about a “direction”), which are used to, for example, model the polarization of photons.

Now, the main point about all these fields is that we need them to encode information about something that may vary throughout space.

These fields can then be used to do integrals and other things that describe various physical, geometric or otherwise interesting phenomena. We will see all of this throughout this course.

Lesson Summary

This lesson has mostly been a short “introduction” to concepts in vector calculus, but here are the key takeaways:

• A scalar field takes in a point in space and outputs a scalar (something with only a magnitude).
• A vector field takes in a point in space and outputs a vector (something with both a magnitude and direction).
• Both scalar and vector fields are generally functions of the coordinates in a given coordinate system.