The Euler-Lagrange Equation & Beltrami Identity

In the last lesson, we discussed functionals and functional variations. Before we get to the topic of this lesson – finding extrema of functionals through the Euler-Lagrange equation and the Beltrami identity – let’s quickly recap the main points about functionals and variations from the previous lesson.

Lesson Contents

Recap of The Previous Lesson: Functionals & Variations

A functional, in the simplest sense, can be thought of as a function of a function – something that takes in a function as its input and returns a number. In other words, for a given function y(x), the functional F(y) assigns a particular number for the function y(x).

We usually express functionals in the form of a definite integral (this has the desired property of returning a single number, given a function):

F\left(y\right)=\int_{x_1}^{x_2}f\left(x{,}\ y{,}\ y'\right)dx — Here, y’ is shorthand for dy/dx, a piece of notation we’ll be using a lot.

The integrand f(x,y,y’) here is what encodes all the important stuff about this functional. In practice, when we’re working with functionals (such as calculating Euler-Lagrange equations), we usually work with just the integrand of the particular functional we’re interested in.

We can also calculate the variation in a functional, which describes how the functional changes if we change its input function y(x), which consequently will also change the y’=dy/dx-term. The variation in a functional, δF, is calculated similarly to the total differential of a multivariable function:

\delta F=\int_{x_1}^{x_2}\delta f\ dx=\int_{x_1}^{x_2}\left(\frac{\partial f}{\partial y}\delta y+\frac{\partial f}{\partial y'}\delta y'\right)dx — Important note; when calculating the variation in a functional, we do NOT vary the “independent variable” (x in this case), only the input function y.

This is pretty much what we covered in the last lesson. This then brings us to the topic of this lesson – if variational calculus is all about finding extrema (minima, maxima, stationary points) of functionals, how do we find these extrema? The answer is from something called the Euler-Lagrange equations.

The Euler-Lagrange Equation

The Euler-Lagrange equation is a fundamental result in calculus of variations that is used to find extrema or stationary points of functionals. Simply put, the Euler-Lagrange equation is the condition that any functional has to satisfy in order for the functional to have a stationary value.

Just to make it very clear, a stationary value or an extremal value of a functional refers to a minimum, a maximum or a “saddle point” of the functional. These are the points at which the variation in the functional is zero (analogous to df/dx=0 defining the stationary points of a single-variable function):

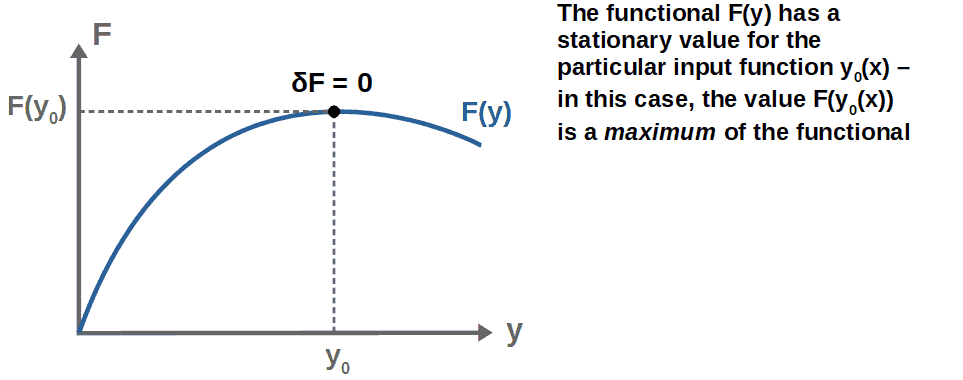
While this may look exactly the same as a graph depicting the maximum of a single-variable function, this is inherently different still. This is because the “variable” y here is not really a variable, it’s an entire function y(x) in itself. However, the same idea still applies here as for a single-variable function – if the functional F(y) takes in the particular input function y₀(x), it will be at a stationary value.

Specifically, if we have a functional F(y) expressed as a definite integral over some integrand function f(x,y,y’), then we will discover that in order for y(x) to be a stationary point of F(y), the integrand function f(x,y,y’) has to satisfy the following condition:

\frac{d}{dx}\frac{\partial f}{\partial y'}-\frac{\partial f}{\partial y}=0

This is the Euler-Lagrange equation applied to a functional of the function y(x). We’ll see where this comes from very soon.

It’s worth mentioning that sometimes we may have a functional of several different functions. For example, say we have a functional of two independent functions, y(x) and z(x):

F\left(y{,}\ z\right)=\int_{x_1}^{x_2}f\left(x{,}\ y{,}\ y'{,}\ z{,}\ z'\right)dx

In this case, we’re going to have one Euler-Lagrange equation for each function, which would both need to be satisfied in order for the particular set of functions, y(x) and z(x), to be at a stationary point of F(y,z):

\frac{d}{dx}\frac{\partial f}{\partial z'}-\frac{\partial f}{\partial z}=0

These Euler-Lagrange equations will then result in two differential equations and we would have to solve both of them simultaneously to find the set of functions y(x) and z(x) that make the given functional stationary.

This kind of thing of having multiple Euler-Lagrange equations is especially common in Lagrangian mechanics, where we have one Euler-Lagrange equation for each coordinate of a given physical system and often, these equations are going to be coupled together in complicated ways.

So, the Euler-Lagrange equation is what we use to obtain extremal “points” of functionals (again, which are not really points but rather functions) – specifically, we do this by plugging the integrand of the specific functional of interest into the Euler-Lagrange equation and solving the resulting differential equations.

We’ll see examples of how this actually works in practice in the next lesson. But first, let’s discuss an extremely important physical application of the Euler-Lagrange equation – namely, how the Euler-Lagrange equation is used in a formulation of classical mechanics called Lagrangian mechanics.

Physics Example: The Euler-Lagrange Equation In Lagrangian Mechanics

In the most simple sense, Lagrangian mechanics is an alternative approach to classical mechanics and to Newton’s laws. Lagrangian mechanics is used to find equations of motion for physical systems, which can then be solved to find predict how the system evolves in time.

This is precisely what Newton’s laws, such as F=ma, do as well. However, it turns out that Lagrangian mechanics is much more powerful than Newtonian mechanics and in fact, it is not just another tool for solving mechanics problems; Lagrangian mechanics is a framework for describing all of physics.

Now, we will talk about Lagrangian mechanics more in a later lesson, but I want to show you a quick “teaser” here. Namely, we will look at how the Euler-Lagrange equation appears as one of the most central equations used in Lagrangian mechanics.

The basic idea of the Lagrangian formulation is that we describe any physical system by first specifying all the so-called generalized coordinates for the system and then write down a function called the Lagrangian. The Lagrangian essentially encodes all the dynamics of that system.

We then obtain the equations of motion automatically from the Lagrangian by applying the Euler-Lagrange equations to each of the generalized coordinates.

Now, the Lagrangian of a system is a function that describes the kinetic and potential energy of the whole system at each point in time (this turns out to be enough for describing everything about the dynamics of the system). The Lagrangian is defined as the difference between kinetic energy (T) and potential energy (V):

The Lagrangian is essentially a function of the coordinates describing a system (usually labeled as q_i), the time derivatives of the coordinates, dq_i/dt (we usually label time derivatives by putting a dot above the variable) and possibly time (t) as well:

L\left(q_i{,}\ \dot{q}_i{,}\ t\right)=T\left(\dot{q}_i{,}\ t\right)-V\left(q_i{,}\ t\right) — Note; we usually take the kinetic energy to be a function of velocity only (and possibly time), while the potential energy is a function of position only (and possibly time).

We then obtain the equations of motion for a system by plugging the Lagrangian of a system into the Euler-Lagrange equation:

\frac{d}{dt}\frac{\partial L}{\partial\dot{q}_i}-\frac{\partial L}{\partial q_i}=0 — Here, we’ve basically replaced the variables x, y and y’ from earlier with t, q_i and q_i-dot (=dq_i/dt). These are the variables we generally use in Lagrangian mechanics.

Now, this might make you wonder whether the Lagrangian is actually the integrand of some functional that is to be optimized, since it appears here in the Euler-Lagrange equation. It indeed is – this functional is called the action, but we’ll discuss this later.

The main point of all of this is that Lagrangian mechanics is a formulation in which we use the Euler-Lagrange equation to obtain the equations of motion for a system. This is done by first constructing a Lagrangian from the kinetic and potential energies of the system.

Let’s look at a quick example to illustrate this. Consider a particle of mass m that can move in one dimension, along the x-axis, let’s say. The particle’s velocity is given by v=dx/dt, so it has kinetic energy:

T=\frac{1}{2}mv^2=\frac{1}{2}m\left(\frac{dx}{dt}\right)^2=\frac{1}{2}m\dot{x}^2 — Here, I’m using the dot notation again to represent a time derivative.

Let’s also say that the particle has some potential energy V(x) that is a function of its position. We can then construct a Lagrangian for this particle as the difference between its kinetic and potential energies:

L=T-V=\frac{1}{2}m\dot{x}^2-V\left(x\right)

The equations of motion for the particle are then obtained by plugging this Lagrangian into the Euler-Lagrange equation (where we now have just one coordinate q_i, which is just x):

\frac{d}{dt}\frac{\partial L}{\partial\dot{x}}-\frac{\partial L}{\partial x}=0

If we now plug the Lagrangian into this, these partial derivatives will give us (note; when calculating these partial derivatives, we treat x and x-dot as independent variables):

\frac{\partial L}{\partial\dot{x}}=\frac{\partial}{\partial\dot{x}}\left(\frac{1}{2}m\dot{x}^2-V\left(x\right)\right)=m\dot{x}

\frac{\partial L}{\partial x}=\frac{\partial}{\partial x}\left(\frac{1}{2}m\dot{x}^2-V\left(x\right)\right)=-\frac{\partial V}{\partial x}

The Euler-Lagrange equation then gives us:

\frac{d}{dt}\frac{\partial L}{\partial\dot{x}}-\frac{\partial L}{\partial x}=0\ \ \Rightarrow\ \ \frac{d}{dt}\left(m\dot{x}\right)-\left(-\frac{\partial V}{\partial x}\right)=0

When taking the time derivative of x-dot, we get the second time derivative of x (d²x/dt²), which we represent by x with two dots. So, from the Euler-Lagrange equation, we finally get:

m\ddot{x}=-\frac{\partial V}{\partial x}

Can you see what this equation is? On the left-hand side, we essentially have mass times the second time derivative of position (i.e. acceleration) and on the right, we practically have the negative gradient of potential energy (which is the definition of a conservative force). So, this equation really reads:

What is the conclusion here? The Euler-Lagrange equation is nothing but Newton’s second law, F=ma, but just written in terms of a Lagrangian. Indeed, for any system we can construct a Lagrangian for, the Euler-Lagrange equation gives us the same equations of motion as F=ma would – the Euler-Lagrange equation is just F=ma in disguise.

In fact, this is the basis for Lagrangian mechanics – it is completely equivalent to Newtonian mechanics, but turns out to be much more powerful and more applicable to other areas of modern physics than Newton’s laws (through this example does not really show that).

Again, we’ll be talking more about Lagrangian mechanics later. Here, I just wanted to show an example of how the Euler-Lagrange equation appears in physics, namely as something we can use to derive equations of motion from by first constructing a function called the Lagrangian.

The next thing you might have is your mind now is – where does the Euler-Lagrange equation actually come from in the first place? How does it relate to the variation of a functional used to determine extremal points we mentioned earlier?

Derivation of The Euler-Lagrange Equation

Just like the stationary points of an ordinary single-variable function are found from the condition that df(x)/dx=0, stationary points (i.e. functions y(x)) of a functional are found by setting the variation to zero, δF=0.

We’ll see next that this condition of the variation of a functional being equal to zero leads exactly to the Euler-Lagrange equation. In this derivation, just to make it clear, we’ll consider functionals of the form:

Now, before we do this, there is an important assumption we need to make. The value of the function y(x) at the end points, x₁ and x₂, should remain fixed – in other words, there is no variation in y(x) at the end points:

\delta y\left(x_1\right)=\delta y\left(x_2\right)=0

Intuitively, this just means that we’re only interested in finding stationary solutions y(x), which have the same start and end points. For example, if we were looking at minimizing the distance between two points, it wouldn’t make sense for these two points themselves to be varied, only the curve in between.

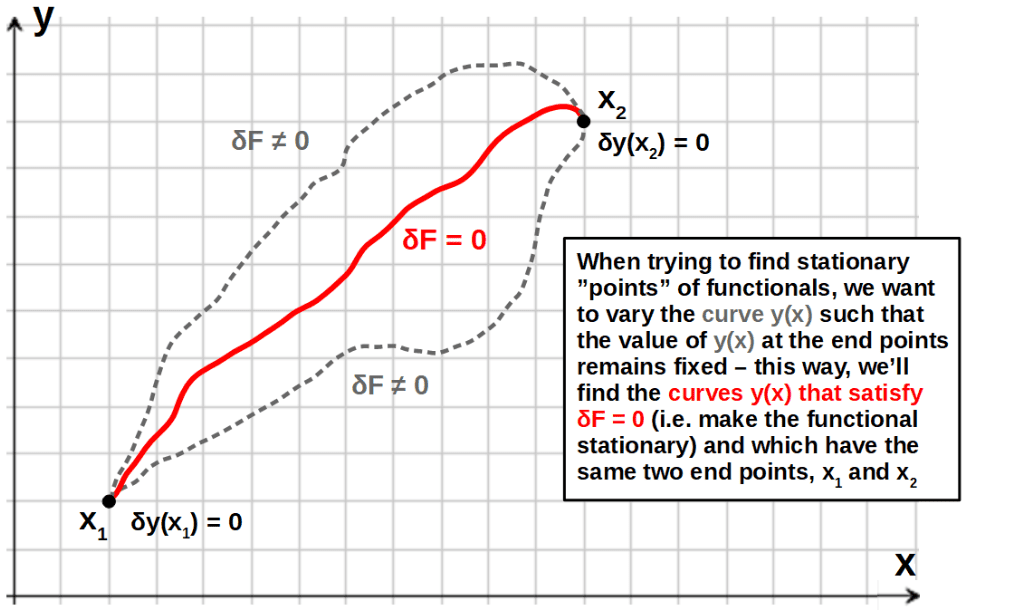
With this assumption, we can derive the Euler-Lagrange equation, which you’ll find down below.

Step-By-Step Derivation of The Euler-Lagrange Equation

We’ll begin with calculating the variation in our functional F(y) – which we will eventually set equal to zero – using the formula from the previous lesson:

\delta F=\int_{x_1}^{x_2}\left(\frac{\partial f}{\partial y}\delta y+\frac{\partial f}{\partial y'}\delta y'\right)dx

Let’s now begin manipulating this expression a little bit – first, consider the following term:

\delta y'=\delta\left(\frac{dy}{dx}\right) — As a reminder; y’ is shorthand notation for dy/dx.

We can move the variation here inside the derivative – this is a valid thing to do, since the functional variation specifically looks at varying the function y and not the independent variable x (as mentioned in the previous lesson) and therefore, the order of the two operations (δ and d/dx) does not matter. We then have:

\delta y'=\frac{d\left(\delta y\right)}{dx}\ \ \Rightarrow\ \ \delta F=\int_{x_1}^{x_2}\left(\frac{\partial f}{\partial y}\delta y+\frac{\partial f}{\partial y'}\frac{d\left(\delta y\right)}{dx}\right)dx

Let’s look at this second term closer. We know from the rule for a derivative of the product of two functions that:

\frac{d}{dx}\left(g\left(x\right)h\left(x\right)\right)=h\frac{dg}{dx}+g\frac{dh}{dx}\ \ \Rightarrow\ \ g\frac{dh}{dx}=\frac{d}{dx}\left(gh\right)-h\frac{dg}{dx}

From this formula, we can just replace g and h with g=∂f/∂y’ and h=δy, so that we have:

\frac{\partial f}{\partial y'}\frac{d\left(\delta y\right)}{dx}=\frac{d}{dx}\left(\frac{\partial f}{\partial y'}\delta y\right)-\frac{d}{dx}\left(\frac{\partial f}{\partial y'}\right)\delta y

This is exactly one of the terms we have in our expression for δF above. So, inserting this, we then have:

\delta F=\int_{x_1}^{x_2}\left(\frac{\partial f}{\partial y}\delta y+\frac{\partial f}{\partial y'}\frac{d\left(\delta y\right)}{dx}\right)dx

\Rightarrow\ \ \delta F=\int_{x_1}^{x_2}\left(\frac{\partial f}{\partial y}\delta y+\frac{d}{dx}\left(\frac{\partial f}{\partial y'}\delta y\right)-\frac{d}{dx}\left(\frac{\partial f}{\partial y'}\right)\delta y\right)dx

We can now split this integral into two parts (since it’s just a sum):

\delta F=\int_{x_1}^{x_2}\left(\frac{\partial f}{\partial y}\delta y-\frac{d}{dx}\left(\frac{\partial f}{\partial y'}\right)\delta y\right)dx+\int_{x_1}^{x_2}\frac{d}{dx}\left(\frac{\partial f}{\partial y'}\delta y\right)dx

In the second term, we’re taking the integral of a derivative and by the fundamental theorem of calculus, the integral and derivative operations basically “cancel” each other. So, this just becomes a substitution of the integration limits. We can also factor out the δy in the first term:

\delta F=\int_{x_1}^{x_2}\delta y\left(\frac{\partial f}{\partial y}-\frac{d}{dx}\frac{\partial f}{\partial y'}\right)dx+\bigg/_{\!\!\!\!\!{x_1}}^{x_2}\left(\frac{\partial f}{\partial y'}\delta y\right)

Now, here is where we use our little assumption from earlier; the variation of y(x) at the start and end points should be zero:

If we now look at the second term in our formula for δF, this term will, in fact, go to zero since it involves substituting the value of δy at x₁ and x₂. So, from substituting these limits of integration, we get:

\bigg/_{\!\!\!\!\!{x_1}}^{x_2}\left(\frac{\partial f}{\partial y'}\delta y\right)=\frac{\partial f}{\partial y'}\left(x_2\right)\delta y\left(x_2\right)-\frac{\partial f}{\partial y'}\left(x_1\right)\delta y\left(x_1\right)=0

We are then left with only the first term in our expression for δF:

\delta F=\int_{x_1}^{x_2}\delta y\left(\frac{\partial f}{\partial y}-\frac{d}{dx}\frac{\partial f}{\partial y'}\right)dx

So far, we haven’t specifically looked at stationary points – we get these by the condition that δF=0 as mentioned previously. We therefore have the following condition:

\delta F=0\ \ \Rightarrow\ \ \int_{x_1}^{x_2}\delta y\left(\frac{\partial f}{\partial y}-\frac{d}{dx}\frac{\partial f}{\partial y'}\right)dx=0

Now, this integral can only be zero at all times if whatever is inside the integral is also zero:

\delta y\left(\frac{\partial f}{\partial y}-\frac{d}{dx}\frac{\partial f}{\partial y'}\right)=0\ \ \Rightarrow\ \ \frac{d}{dx}\frac{\partial f}{\partial y'}-\frac{\partial f}{\partial y}=0

This, of course, is just the Euler-Lagrange equation, which completes our derivation.

Now, the point of the above derivation was to show that for any functional F(y) written in the form of a definite integral over some integrand function f(x,y,y’) to be stationary, its integrand f has to satisfy the Euler-Lagrange equation.

This gives us a practical way to find the functions y(x) that make any given functional stationary – all we do is plug a specific f(x,y,y’) into the Euler-Lagrange equation, calculate some derivatives and solve the resulting differential equation for y(x). We’ll see some examples of this in the next lesson.

The Beltrami Identity

It’s worth going over a really useful special case of the Euler-Lagrange equation – the Beltrami identity.

The Beltrami identity applies whenever we have a functional F(y) in which the integrand f does not explicitly depend on the variable x. In other words, it is of the form f(y,y’). Of course, y and y’ still do depend on x, so the integrand still depends on x implicitly.

It turns out that quite many functionals are actually of this form and whenever they are, the Euler-Lagrange equation can be significantly simplified.

Now, mathematically, the statement that f does not explicitly depend on x means that ∂f/∂x=0. Whenever this is true, we can prove that the Euler-Lagrange equation reduces to the following form:

This is called the Beltrami identity. It is a special case of the Euler-Lagrange equation and it applies whenever we have ∂f/∂x=0.

Now, why is the Beltrami identity useful? Well, in many cases where it’s applicable, it’s much simpler to use than the Euler-Lagrange equation – the Beltrami identity only requires us to take a single derivative, namely ∂f/∂y’, and nothing else.

The Beltrami identity also results in first-order differential equations instead of second-order differential equations, which the Euler-Lagrange equation would give us. These, of course, are generally much easier to solve.

So, the Beltrami identity is a useful special case of the Euler-Lagrange equation, which can be used in certain situations to greatly simplify things.

The Beltrami identity also has a very interesting physical interpretation much like the Euler-Lagrange equation. In fact, the Beltrami identity turns out to represent energy conservation in classical mechanics – it also gives us a function called the Hamiltonian, which is used extensively in modern physics. You’ll find more discussion on this below.

Physics Example: The Beltrami Identity In Hamiltonian Mechanics

Earlier, we discovered that the Euler-Lagrange equation is essentially Newton’s second law, F=ma, but written in a slightly different form. Now, what would the physical meaning of the Beltrami identity be?

The easiest way to see this is to consider again our simple example of a 1D particle moving along the x-axis under some potential V(x). This particle is described by the following Lagrangian (from earlier):

L=\frac{1}{2}m\dot{x}^2-V\left(x\right) — Here, x with a dot above it represents the time derivative of x, dx/dt, again. This is the velocity of the particle.

The Beltrami identity applies whenever we have ∂L/∂t=0 (since our quantities in this are L and t instead of f and x like we had previously). We can see that this Lagrangian does not contain any term with t in it explicitly, so the Beltrami identity is applicable for this Lagrangian.

Let’s plug this Lagrangian into the Beltrami identity (with y’ now being replaced by x-dot, since that’s our variable of interest in this case):

\frac{\partial L}{\partial\dot{x}}\dot{x}-L=C

\Rightarrow\ \ \frac{\partial}{\partial\dot{x}}\left(\frac{1}{2}m\dot{x}^2-V\left(x\right)\right)\dot{x}-\left(\frac{1}{2}m\dot{x}^2-V\left(x\right)\right)=C

\Rightarrow\ \ \left(m\dot{x}\right)\dot{x}-\frac{1}{2}m\dot{x}^2+V\left(x\right)=C

\Rightarrow\ \ m\dot{x}^2-\frac{1}{2}m\dot{x}^2+V\left(x\right)=C

\Rightarrow\ \ \frac{1}{2}m\dot{x}^2+V\left(x\right)=C

Do you recognize what this quantity is on the left-hand side? It is the sum of kinetic energy and potential energy – the total energy of the particle! What this equation then tells us is that the energy of the particle is a constant C, so it is conserved.

Physically, this means that whenever a Lagrangian is explicitly time-independent (i.e. ∂L/∂t=0), the total energy of the system is conserved (constant). The total energy of the system in that case is given by the left-hand side of the Beltrami identity:

E=\frac{\partial L}{\partial\dot{x}}\dot{x}-L

Or more generally, if expressed in terms of the generalized coordinates of the system (q_i), this would be:

E=\sum_i^{ }\frac{\partial L}{\partial\dot{q}_i}\dot{q}_i-L

Now, what happens if the Lagrangian of a system is not time-independent (i.e. ∂L/∂t≠0)? In that case, the Beltrami identity does not apply and physically, it turns out that the left-hand side of the Beltrami identity, in general, does not represent the total energy of the system and the right-hand side will, in general, not be constant.

However, even if this is the case, we can still define a function H that is of the form:

H=\sum_i^{ }\frac{\partial L}{\partial\dot{q}_i}\dot{q}_i-L

This function is generally called the Hamiltonian and it is the basis for a completely different formulation of mechanics known as Hamiltonian mechanics (which is equivalent to both Lagrangian and Newtonian mechanics).

But what does the Hamiltonian of a system actually represent? Well, that depends.

In particular, if the Lagrangian of a given system does not explicitly depend on time (∂L/∂t=0), then the Beltrami identity is applicable and this means that the Hamiltonian of that given system is constant:

H=\sum_i^{ }\frac{\partial L}{\partial\dot{q}_i}\dot{q}_i-L=C

If this is the case, the Hamiltonian represents the total energy of the system and is conserved (like we saw in the 1D particle example). However, if the Lagrangian does explicitly depend on time (∂L/∂t≠0), the Beltrami identity is not true anymore and we will generally have:

H=\sum_i^{ }\frac{\partial L}{\partial\dot{q}_i}\dot{q}_i-L\ne C

In this case, the Hamiltonian does not represent the energy of the system and is not conserved, but it is still an extremely useful function.

In fact, the Hamiltonian can also be used to find the equations of motion for a system, regardless of whether the Beltrami identity applies or not (in Hamiltonian mechanics, this is done through something called Hamilton’s equations).

The Beltrami identity simply gives a condition for whether the Hamiltonian represents the conserved total energy of a system – namely, whenever the Lagrangian of a system does not explicitly depend on time, the Hamiltonian of the system is conserved (however, it turns out that even if the Beltrami identity is true and the Hamiltonian is conserved, the Hamiltonian still might not physically represent the total energy of the system).

The usefulness of the Hamiltonian is that it is often taken as the definition of energy in modern physics. For example, we can use the Hamiltonian to define the energy density of a field or derive formulas for relativistic energy (such as E=mc²) from the definition of the Hamiltonian.

The Beltrami identity is not too difficult to derive. All we do is manipulate the Euler-Lagrange equation and then apply the condition for the Beltrami identity to be true in the first place:

You’ll find this done step-by-step below.

Step-By-Step Derivation of The Beltrami Identity

Let’s look at exactly how the Beltrami identity is obtained from the Euler-Lagrange equation:

First, let’s multiply everything by y’:

y'\frac{d}{dx}\frac{\partial f}{\partial y'}-\frac{\partial f}{\partial y}y'=0\ \ \ \ \ \ \ \left(1\right)

I’ve labeled this equation (1), since we’ll come back to it soon. But first, let’s consider taking the total derivative of f(x,y,y’) with respect to x. This total derivative will have contributions coming from x, y and y’, which we can calculate by the chain rule:

\frac{df}{dx}=\frac{\partial f}{\partial x}+\frac{\partial f}{\partial y}\frac{dy}{dx}+\frac{\partial f}{\partial y'}\frac{d\left(y'\right)}{dx}=\frac{\partial f}{\partial x}+\frac{\partial f}{\partial y}y'+\frac{\partial f}{\partial y'}y''

Let’s now move some terms around to solve for (∂f/∂y)y’ (you’ll see why soon):

\frac{\partial f}{\partial y}y'=\frac{df}{dx}-\frac{\partial f}{\partial x}-\frac{\partial f}{\partial y'}y''

This is exactly one of the terms we have in equation (1). So, let’s insert this into (1):

\Rightarrow\ \ y'\frac{d}{dx}\frac{\partial f}{\partial y'}-\left(\frac{df}{dx}-\frac{\partial f}{\partial x}-\frac{\partial f}{\partial y'}y''\right)=0

\Rightarrow\ \ y'\frac{d}{dx}\frac{\partial f}{\partial y'}+\frac{\partial f}{\partial y'}y''=\frac{df}{dx}-\frac{\partial f}{\partial x}

Here I’ve purposefully moved some of the terms to the right-hand side, since you may now be able to see that the left-hand side has exactly the form of a derivative of a product of two terms (using the product rule for derivatives):

y'\frac{d}{dx}\frac{\partial f}{\partial y'}+\frac{\partial f}{\partial y'}y''=\frac{d}{dx}\left(\frac{\partial f}{\partial y'}y'\right)

So, the above equation then becomes:

\frac{d}{dx}\left(\frac{\partial f}{\partial y'}y'\right)=\frac{df}{dx}-\frac{\partial f}{\partial x}

We now use the assumption of the Beltrami identity that ∂f/∂x=0 (i.e. f does not explicitly depend on x), which reduces our equation to:

\frac{d}{dx}\left(\frac{\partial f}{\partial y'}y'\right)=\frac{df}{dx}

We now have a total derivative d/dx on both sides, so we can simply integrate and use the fundamental theorem of calculus to get:

\int_{ }^{ }\frac{d}{dx}\left(\frac{\partial f}{\partial y'}y'\right)dx=\int_{ }^{ }\frac{df}{dx}dx\ \ \Rightarrow\ \ \frac{\partial f}{\partial y'}y'=f+C

Here, C is an arbitrary integration constant that can be found from the boundary conditions of any given problem. In any case, moving f to the other side now completes our derivation of the Beltrami identity:

As you can see from this derivation, the Beltrami identity is obtained from the Euler-Lagrange equation in the case that ∂f/∂x=0.

Vector Calculus For Physics: A Complete Self-Study Course

The Euler-Lagrange Equation & Beltrami Identity

Recap of The Previous Lesson: Functionals & Variations

The Euler-Lagrange Equation

Derivation of The Euler-Lagrange Equation

The Beltrami Identity

Modal title